1. Introduction▲
1-1. Les types de données natifs▲
En Python, toute valeur appartient à une classe qui détermine son type de valeur. Les valeurs qui partagent une classe partagent également le comportement. Par exemple, les nombres entiers 1 et 2 sont les deux instances de la classe int. Ces deux valeurs peuvent être traitées de façon similaire. Par exemple, on peut prendre leur valeur opposée (négative) ou bien les ajouter à un autre nombre entier. La fonction intégrée type nous permet d'inspecter la classe de n'importe quelle valeur.
>>> type ( 2 )
<class 'int'>Les valeurs que nous avons utilisées jusqu'ici sont des exemples d'un petit nombre de types de données natifs intégrés dans le langage Python. Les types de données natifs présentent les propriétés suivantes :
- Il existe des expressions qui s'évaluent à des valeurs appartenant à des types natifs, appelés littéraux.
- Il existe des fonctions et des opérateurs intégrés permettant de manipuler des valeurs de types natifs.
La classe int est le type de données natif utilisé pour représenter des nombres entiers. Les littéraux entiers (séquences de chiffres adjacents) s'évaluent aux valeurs int, et les opérateurs mathématiques manipulent ces valeurs.
>>> 12 + 3000000000000000000000000
3000000000000000000000012Python possède trois types numériques natifs : les nombres entiers (int), les nombres réels (float) et les nombres complexes (complex).
Les floats. Le nom float provient de la façon dont les nombres réels sont représentés en Python et dans de nombreux autres langages de programmation : une représentation dite « à virgule flottante ». Les détails de la façon dont ces nombres sont représentés ne sont pas le sujet de ce cours, mais il est important de connaître certaines différences de haut niveau entre les objets int et float. En particulier, les objets de type int représentent des entiers exactement, sans aucune approximation ni limite à leur taille. En revanche, les objets de type float peuvent représenter une large gamme de nombres fractionnaires, mais tous les nombres ne peuvent pas être représentés exactement, et il existe des valeurs minimales et maximales. Par conséquent, il faut considérer les valeurs de type float comme des approximations des valeurs réelles. Ces approximations n'ont qu'une précision limitée. La combinaison des valeurs de type float peut entraîner des erreurs d'approximation ; les deux expressions suivantes s'évalueraient à 7 s'il n'y avait pas d'approximation.
>>> 7 / 3 * 3
7.0
>>> 1 / 3 * 7 * 3
6.999999999999999Bien que les expressions ci-dessus combinent des valeurs de type int, la division d'un int par un nombre d’un autre type produit une valeur de type float : une approximation finie et tronquée du quotient réel des deux nombres entiers divisés.
>>> type(1/3)
<class 'float'>
>>> 1/3
0.3333333333333333Cette approximation conduit à des problèmes lorsque nous effectuons des tests d'égalité.
>>> 1/3 == 0.333333333333333312345 # Gare à l'approximation du float
TrueCes différences subtiles entre la classe int et float ont des conséquences importantes pour l'écriture de programmes, et ce sont des détails que les programmeurs doivent mémoriser. Heureusement, il n'y a qu'une poignée de types de données natifs, ce qui limite la quantité de choses à mémoriser pour devenir compétent dans un langage de programmation. En outre, ces détails sont à peu près les mêmes dans de nombreux langages de programmation, qui appliquent généralement des normes telles qu’appliquées par des directives communautaires telles que la norme IEEE 754 de représentation des nombres à virgule flottante.
Types non numériques. Les valeurs peuvent représenter de nombreux autres types de données, tels que des sons, des images, des lieux, des adresses Web, des connexions réseau et ainsi de suite. Certaines sont représentées par des types de données natifs, comme la classe Bool pour les valeurs True et False. Mais pour la plupart des valeurs, il incombe au développeur de définir ses propres types en utilisant les moyens de combinaison et d'abstraction que nous développerons dans ce chapitre.
La suite de ce tutoriel présente d'autres types de données natifs de Python, en se concentrant surtout sur le rôle qu'ils jouent dans la création d'abstractions de données utiles. Vous pouvez trouver plus de détails sur les différents types natifs dans la documentation officielle de Python 3.
2. Abstraction de données▲
Si nous considérons le vaste ensemble de choses dans le monde que nous aimerions représenter dans nos programmes, nous constatons que la plupart d'entre elles ont une structure composée. Par exemple, une position géographique a des coordonnées de latitude et de longitude. Pour représenter des positions, nous aimerions que notre langage de programmation nous permette d'associer une latitude et une longitude pour former une paire, une valeur de donnée composée que nos programmes peuvent manipuler en tant qu'entité conceptuelle unique, mais qui comporte également deux parties susceptibles d'être considérées séparément.
L'utilisation de données composées nous permet d'augmenter la modularité de nos programmes. Si nous pouvons manipuler les positions géographiques comme des valeurs entières, nous pouvons protéger des parties de notre programme qui manipulent les positions de celles qui traitent le détail de la représentation de ces positions. La technique générale consistant à isoler les parties d'un programme qui traite de la façon dont les données sont représentées de celles qui traitent de la façon dont les données sont manipulées est une méthodologie de conception puissante appelée abstraction de données. L'abstraction des données rend les programmes beaucoup plus faciles à concevoir, à maintenir et à modifier.
L'abstraction des données est semblable à l'abstraction fonctionnelle. Lorsque nous créons une abstraction fonctionnelle, les détails de la mise en œuvre d'une fonction peuvent être supprimés et la fonction particulière elle-même peut être remplacée par toute autre fonction avec le même comportement global. Autrement dit, nous pouvons créer une abstraction qui sépare la manière dont la fonction est utilisée des détails de sa mise en œuvre. De même, l'abstraction des données isole la façon dont une valeur de données composée est utilisée des détails de la façon dont elle est construite.
L'idée de base de l'abstraction des données est de structurer les programmes de sorte qu'ils fonctionnent sur des données abstraites. C'est-à-dire que nos programmes doivent utiliser les données de sorte à faire aussi peu d'hypothèses que possible sur les données. Parallèlement, une représentation concrète des données est définie comme une partie indépendante du programme.
Ces deux parties d'un programme, la partie qui fonctionne sur des données abstraites et celle qui définit une représentation concrète, sont reliées par un petit ensemble de fonctions qui mettent en place des données abstraites sous la forme d'une représentation concrète. Pour illustrer cette technique, nous allons examiner comment concevoir un ensemble de fonctions pour manipuler des nombres rationnels.
2-1. Exemple : les nombres rationnels▲
En mathématiques, un nombre rationnel est un nombre qui peut s'exprimer comme le quotient de deux nombres entiers. Les nombres rationnels constituent un sous-ensemble important des nombres réels. Un nombre rationnel tel que 1/3 ou 17/29 est généralement écrit comme suit :
<Numérateur> / <dénominateur>dans lequel <numérateur> et <dénominateur> représentent des valeurs entières. Les deux parties sont nécessaires pour caractériser exactement la valeur du nombre rationnel. Si l'on effectue réellement la division des nombres entiers, on obtient une approximation de type float, et l'on perd la précision exacte des nombres entiers.
>>> 1/3
0.3333333333333333
>>> 1/3 == 0.333333333333333300000 # La division d'entiers donne une approximation
TrueCependant, nous pouvons créer une représentation exacte pour les nombres rationnels en combinant le numérateur et le dénominateur.
Nous avons constaté en utilisant des abstractions fonctionnelles que nous pouvons commencer à programmer de manière productive avant de mettre en œuvre certaines parties de notre programme. Commençons par supposer que nous ayons déjà un moyen de construire un nombre rationnel à partir d'un numérateur et d'un dénominateur. Supposons également qu'étant donné un nombre rationnel, nous ayons un moyen de retrouver le numérateur et le dénominateur qui le constituent. Supposons en outre que le constructeur et les sélecteurs soient disponibles comme les trois fonctions suivantes :
- rational (n, d) renvoie le nombre rationnel dont le numérateur est n et le dénominateur d.
- numer (x) renvoie le numérateur du nombre rationnel x.
- denom (x) renvoie le dénominateur du nombre rationnel x.
Nous utilisons ici une stratégie puissante de conception de programmes : des vœux pieux. Nous n'avons pas encore dit comment est représenté un nombre rationnel, ni comment les fonctions numer, denom et rational doivent être mises en œuvre. Pourtant, si nous définissions ces trois fonctions, nous pourrons ajouter, multiplier, imprimer et tester l'égalité des nombres rationnels :
>>> def add_rationals(x, y):
nx, dx = numer(x), denom(x)
ny, dy = numer(y), denom(y)
return rational(nx * dy + ny * dx, dx * dy)
>>> def mul_rationals(x, y):
return rational(numer(x) * numer(y), denom(x) * denom(y))
>>> def print_rational(x):
print(numer(x), '/', denom(x))
>>> def rationals_are_equal(x, y):
return numer(x) * denom(y) == numer(y) * denom(x)Nous avons maintenant les opérations sur des nombres rationnels définies à l'aide des fonctions de sélection, numer et denom, et du constructeur rational, mais nous n'avons pas encore défini ces fonctions. Ce dont nous avons besoin, c'est d'un moyen d'assembler un numérateur et un dénominateur en une valeur composite.
2-2. Les paires▲
Pour nous permettre de mettre en œuvre le niveau concret de notre abstraction de données, Python fournit une structure composée appelée list, qui peut être construite en plaçant les expressions entre crochets séparées par des virgules. Une telle expression s'appelle une liste littérale.
>>> [ 10 , 20 ]
[10, 20]Il existe deux façons de consulter les éléments d'une liste. La première est notre méthode familière d'affectation multiple, qui décompose une liste en ses éléments individuels et lie chaque élément à un autre nom.
>>> pair = [10, 20]
>>> pair
[10, 20]
>>> x, y = pair
>>> x
10
>>> y
20Une deuxième méthode pour accéder aux éléments d'une liste est par l'utilisation d'un indice placé entre crochets. Contrairement à une liste littérale, une expression entre crochets suivant directement une autre expression ne s'évalue pas à une valeur de liste, mais sélectionne un élément à partir de la valeur de l'expression précédente.
>>> pair[0]
10
>>> pair[1]
20Les listes Python (et les séquences ou tableaux dans la plupart des autres langages de programmation) ont un indice qui commence à 0, ce qui signifie que l'indice 0 sélectionne le premier élément de la liste, l'indice 1 sélectionne le second, et ainsi de suite. Une intuition qui supporte cette convention d'indexation est que l'indice représente le décalage d'un élément par rapport au début de la liste.
La fonction équivalente à l'opérateur crochets d'indiçage d'élément s'appelle getitem, et elle utilise également des indices commençant à 0 pour sélectionner les éléments d'une liste.
>>> from operator import getitem
>>> getitem(pair, 0)
10
>>> getitem(pair, 1)
20Les listes à deux éléments ne sont pas la seule méthode de représentation de paires de Python. Toute façon de regrouper deux valeurs peut être considérée comme une paire. Les listes sont une méthode courante pour le faire. Les listes peuvent également contenir plus de deux éléments, comme nous le verrons plus loin dans ce tutoriel.
Représenter des nombres rationnels. Nous pouvons maintenant représenter un nombre rationnel par deux entiers : un numérateur et un dénominateur.
>>> def rational(n, d):
return [n, d]
>>> def numer(x):
return x[0]
>>> def denom(x):
return x[1]Avec les opérations arithmétiques que nous avons définies plus tôt, nous pouvons maintenant manipuler des nombres rationnels avec les fonctions que nous avons définies.
>>> half = rational(1, 2)
>>> print_rational(half)
1 / 2
>>> third = rational(1, 3)
>>> print_rational(mul_rationals(half, third))
1 / 6
>>> print_rational(add_rationals(third, third))
6 / 9Comme le montre l'exemple ci-dessus, notre implémentation des nombres rationnels ne simplifie pas les nombres rationnels à leur fraction irréductible. Nous pouvons remédier à cette lacune en modifiant la mise en œuvre de la fonction rational. Si nous avons une fonction permettant de calculer le plus grand dénominateur commun (PGDC) de deux entiers, nous pouvons l'utiliser pour simplifier le numérateur et le dénominateur et obtenir une fraction irréductible avant de construire la paire. Comme pour beaucoup d'outils utiles, une telle fonction existe déjà dans la bibliothèque Python et s'appelle gcd :
>>> from fractions import gcd
>>> def rational(n, d):
g = gcd(n, d)
return (n//g, d//g)L'opérateur de division entière, //, exprime la division entière, qui arrondit la partie fractionnaire du résultat de division. Puisque nous savons que g est un diviseur commun de n et de d, la division entière est exacte dans ce cas. Cette nouvelle mise en œuvre de rational garantit que les nombres rationnels sont exprimés sous la forme de fractions irréductibles.
>>> print_rational(add_rationals(third, third))
2 / 3Cette amélioration s'est faite en modifiant le constructeur sans changer les fonctions qui implémentent les opérations arithmétiques réelles.
2-3. Les barrières entre abstractions▲
Avant de poursuivre avec d'autres exemples de données composées et d'abstraction de données, considérons certaines des questions soulevées par l'exemple des nombres rationnels. Nous avons défini les opérations en termes du constructeur rational et de sélecteurs numer et denom. En général, l'idée sous-jacente de l'abstraction de données est d'identifier un ensemble d'opérations de base dans lequel s'exprimeront toutes les manipulations de valeurs d'un certain genre, puis d'utiliser uniquement ces opérations de manipulation des données. En limitant l'utilisation des opérations de cette façon, il est beaucoup plus facile de modifier la représentation des données abstraites sans modifier le comportement d'un programme.
Pour les nombres rationnels, différentes parties du programme manipulent des nombres rationnels en utilisant différentes opérations, comme décrit dans ce tableau.
|
Parties du programme qui… |
Traitent les rationnels comme |
En utilisant seulement |
|
Utilisent les rationnels pour effectuer des calculs |
Valeurs rationnelles entières |
add_rational, mul_rational, rationals_are_equal, print_rational |
|
Créent des rationnels ou instaurent les opérations entre rationnels |
Des numérateurs et des dénominateurs |
rational, numer, denom |
|
Mettent en œuvre des sélecteurs et des constructeurs pour les rationnels |
Listes à deux éléments |
Listes littérales et indices |
Dans chaque couche ci-dessus, les fonctions de la dernière colonne forment une barrière abstractionnelle. Ces fonctions sont appelées par un niveau supérieur et implémentées en utilisant un niveau d'abstraction inférieur.
Une violation de cette barrière se produit chaque fois qu'une partie du programme qui pourrait utiliser une fonction de niveau supérieur utilise plutôt une fonction de niveau inférieur. Par exemple, il est souhaitable, pour écrire une fonction qui calcule le carré d'un nombre rationnel, d'utiliser mul_rational, ce qui ne présuppose rien sur la mise en œuvre interne d'un nombre rationnel.
>>> def square_rational(x):
return mul_rational(x, x)Se référer directement aux numérateurs et dénominateurs violerait une barrière d'abstraction :
>>> def square_rational_violating_once(x):
return rational(numer(x) * numer(x), denom(x) * denom(x))Supposer que les rationnels sont représentés par des listes à deux éléments violerait deux barrières d'abstraction :
>>> def square_rational_violating_twice(x):
return [x[0] * x[0], x[1] * x[1]]Les barrières d'abstraction rendent les programmes plus faciles à maintenir et à modifier. Moins les fonctions dépendent d'une représentation particulière, moins il y a de changements à faire lorsque l'on veut modifier cette représentation. Ces trois implémentations de square_rational renvoient le résultat correct, mais seule la première est robuste pour les changements à venir. La fonction square_rational ne nécessiterait pas de mise à jour même si nous avons modifié la représentation des nombres rationnels. En revanche, square_rational_violating_once devrait être modifié chaque fois que les signatures du sélecteur ou du constructeur ont changé, et square_rational_violating_twice nécessiterait une mise à jour chaque fois que la mise en œuvre interne de nombres rationnels a changé.
2-4. Les propriétés des données▲
Les barrières d'abstraction façonnent la manière dont nous pensons aux données. Une représentation valide d'un nombre rationnel ne se limite pas à une mise en œuvre particulière (comme une liste à deux éléments) ; c'est une valeur renvoyée par rational qui peut être transmise à numer et denom. En outre, la relation appropriée doit s'appliquer au constructeur et aux sélecteurs. À savoir, si nous construisons un nombre rationnel x à partir des entiers n et d, alors il faut que numer (x) / denom (x) soit égal à n / d.
En général, nous pouvons exprimer des données abstraites en utilisant une collection de sélecteurs et constructeurs, ainsi que certaines propriétés de comportement. Tant que les propriétés de comportement sont satisfaites (par exemple, la propriété de division ci-dessus), les sélecteurs et les constructeurs constituent une représentation valide d'une sorte de données. Les détails de mise en œuvre sous une barrière d'abstraction peuvent changer, mais si le comportement ne l'est pas, l'abstraction des données reste valide et tout programme écrit à l'aide de cette abstraction de données restera correct.
Ce point de vue peut être appliqué de manière générale, y compris les valeurs de paires que nous avons utilisées pour implémenter des nombres rationnels. Nous n'avons jamais vraiment dit beaucoup de choses sur ce qu'était une paire, seulement que le langage fournissait les moyens de créer et de manipuler des listes à deux éléments. Le comportement dont nous avons besoin pour implémenter une paire, c'est qu'il assemble deux valeurs. Si l'on énonce la propriété de comportement comme suit :
- Si une paire p a été construite à partir des valeurs x et y, alors select(p, 0) renvoie x et select(p, 1) retourne y.
Alors nous n'avons pas besoin du type de liste pour créer des paires. Au lieu de cela, nous pouvons mettre en place deux fonctions pair et select qui répondent à cette description tout comme une liste à deux éléments :
>>> def pair(x, y):
"""Renvoie une fonction qui représente une paire."""
def get(index):
if index == 0:
return x
elif index == 1:
return y
return get
>>> def select(p, i):
"""Renvoie l'élément d'indice i de la paire p."""
return p(i)Avec cette mise en œuvre, nous pouvons créer et manipuler des paires :
>>> p = pair(20, 14)
>>> select(p, 0)
20
>>> select(p, 1)
14Cette utilisation de fonctions d'ordre supérieur ne correspond nullement à notre notion intuitive de ce que devraient être les données. Néanmoins, ces fonctions suffisent à représenter des paires dans nos programmes. Les fonctions sont suffisantes pour représenter les données composées.
La raison pour laquelle nous montrons cette représentation fonctionnelle d'une paire n'est pas que Python fonctionne réellement de cette façon (il est préférable d'utiliser directement des listes, pour des raisons d'efficacité), mais que cela peut fonctionner de cette façon. La représentation fonctionnelle, bien qu'un peu obscure, est un moyen parfaitement adapté pour représenter les paires, car elle remplit les seules conditions que les paires doivent satisfaire. La pratique de l'abstraction des données nous permet de changer facilement les représentations sous-jacentes.
3. Les séquences▲
Une séquence est une collection ordonnée de valeurs. La séquence est une abstraction puissante et fondamentale en informatique. Les séquences ne sont pas des instances d'un type intégré du langage, ni une représentation abstraite des données, mais plutôt d'une collection de comportements partagés entre plusieurs types de données. Autrement dit, il existe de nombreux types de séquences, mais ils partagent tous un comportement commun. En particulier,
Longueur. Une séquence a une longueur finie. Une séquence vide a une longueur de 0.
Sélection de l'élément. Une séquence a un élément correspondant à un indice entier non négatif et inférieur à sa longueur ; les indices commencent à 0, pour le premier élément.
Python comprend plusieurs types de données natives qui sont des séquences, dont la plus importante est la liste.
3-1. Les listes▲
Une valeur de type list est une séquence qui peut avoir une longueur arbitraire. Les listes ont un large ensemble de comportements intégrés, ainsi qu'une syntaxe spécifique pour exprimer ces comportements. Nous avons déjà vu la liste littérale, qui s'évalue à une instance de list, ainsi qu'une expression de sélection d'élément qui évalue une valeur dans la liste. La fonction intégrée len renvoie la longueur d'une séquence. Ci-dessous, digits est une liste comportant quatre éléments. L'élément à l'indice 3 est le second 8.
>>> digits = [1, 8, 2, 8]
>>> len(digits)
4
>>> digits[3]
8De plus, les listes peuvent être additionnées et multipliées par des nombres entiers. Pour les séquences, l'addition et la multiplication n'additionnent ni ne multiplient les éléments, mais combinent et répliquent les séquences elles-mêmes. C'est-à-dire que la fonction add du module operator (et l'opérateur +) produit une liste qui est la concaténation des arguments ajoutés. La fonction mul du module operator (et l'opérateur *) peut prendre une liste et un entier k pour renvoyer la liste qui consiste en k répétitions de la liste d'origine.
>>> [2, 7] + digits * 2
[2, 7, 1, 8, 2, 8, 1, 8, 2, 8]Une liste peut contenir toutes sortes de valeurs, y compris une autre liste. La sélection d'élément peut être appliquée à plusieurs reprises afin de sélectionner un élément profondément imbriqué dans une liste contenant des listes.
>>> pairs = [[10, 20], [30, 40]]
>>> pairs[1]
[30, 40]
>>> pairs[1][0]
303-2. Itération sur une séquence▲
Bien souvent, nous souhaitons itérer sur les éléments d'une séquence et effectuer un calcul pour chaque élément. Ce modèle est tellement courant que Python possède une instruction de contrôle supplémentaire pour traiter les données séquentielles : l'instruction for.
Considérons le problème de compter combien de fois une valeur apparaît dans une séquence. Nous pouvons implémenter une fonction pour calculer ce compte en utilisant une boucle while.
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total, index = 0, 0
while index < len(s):
if s[index] == value:
total = total + 1
index = index + 1
return total
>>> count(digits, 8)
2L'instruction Python for peut simplifier ce corps de fonction en itérant sur les valeurs des éléments directement sans utiliser de variable index.
>>> def count(s, value):
"""Count the number of occurrences of value in sequence s."""
total = 0
for elem in s:
if elem == value:
total = total + 1
return total
>>> count(digits, 8)
2L'instruction for comprend une seule clause de la forme :
for <name> in <expression>:
<suite>L'instruction for est exécutée par la procédure suivante :
- Évaluez l'<expression> de l'en-tête, qui doit générer une valeur itérative.
-
Pour chaque élément dans cette valeur itérative, dans l'ordre :
- Liez <nom> à cette valeur dans la trame actuelle.
- Exécutez la <suite>.
Cette procédure d'exécution se réfère à des valeurs itérables. Les listes sont un type de séquence, et les séquences sont des valeurs itérables. Leurs éléments sont considérés dans leur ordre séquentiel. Python possède d'autres types itérables, mais nous nous concentrerons sur les séquences pour l'instant. La définition générale du terme « itérable » apparaît dans la section sur les itérateurs du chapitre 4.
Une conséquence importante de cette procédure d'évaluation est que <nom> sera lié au dernier élément de la séquence après l'exécution de l'instruction for. La boucle for introduit une autre manière de mettre à jour l'environnement par une instruction.
Dépaquetage de séquence. Un modèle commun dans les programmes est d'avoir une séquence d'éléments qui sont eux-mêmes des séquences, mais ont tous une longueur fixe. Une déclaration peut inclure plusieurs noms dans son en-tête pour « dépaqueter » chaque séquence d'éléments dans ses éléments respectifs. Par exemple, nous pouvons avoir une liste de listes à deux éléments :
>>> pairs = [[1, 2], [2, 2], [2, 3], [4, 4]]et souhaiter trouver le nombre de ces paires qui ont le même premier et deuxième élément :
>>> same_count = 0L'instruction for suivante liera chaque nom x et y aux premier et second éléments de chaque paire, respectivement :
>>> for x, y in pairs:
if x == y:
same_count = same_count + 1
>>> same_count
2Ce modèle de liaison de noms multiples à plusieurs valeurs dans une séquence à longueur fixe est parfois appelé dépaquetage ou décompactage de séquence ; c'est le même modèle que l'on voit dans les instructions d'affectation qui lient plusieurs noms à plusieurs valeurs.
Intervalles. Un intervalle est un autre type de séquence intégrée dans Python, qui représente un intervalle d'entiers consécutifs. Ces plages de nombres sont créées avec le mot-clef range, qui prend deux arguments entiers : le premier nombre de la série et le nombre immédiatement au-dessus du dernier nombre dans la plage souhaitée.
L'appel du constructeur de liste sur un intervalle s'évalue à une liste ayant les mêmes éléments que l’intervalle, afin que les éléments puissent être facilement inspectés.
Si un seul argument est donné, il est interprété comme le majorant de la dernière valeur pour une plage qui commence à 0.
Les intervalles apparaissent souvent dans l'en-tête d'une boucle for pour spécifier le nombre de fois que la suite de la boucle doit être exécutée : une convention commune consiste à utiliser un caractère de soulignement unique pour le nom dans l'en-tête lorsque le nom n'est pas utilisé dans le corps de la boucle :
>>> for _ in range(3):
print('Go Bears!')
Go Bears!
Go Bears!
Go Bears!Ce caractère de soulignement est juste un nom de variable comme un autre dans l'environnement du point de vue de l'interpréteur, mais il a pour les programmeurs une signification conventionnelle qui indique que ce nom n'apparaîtra pas ailleurs dans la boucle.
3-3. Traitement des séquences▲
Les séquences sont une forme si commune de données composées que des programmes entiers sont souvent organisés autour de cette abstraction unique. Il est possible d'assembler des composants modulaires qui prennent des séquences en entrée et produisent d'autres séquences en sortie pour effectuer le traitement des données. On peut souvent définir des composants complexes en enchaînant un pipeline d'opérations élémentaires de traitement de séquences.
Listes en compréhension. De nombreuses opérations de traitement de séquence peuvent être exprimées en évaluant une expression fixe pour chaque élément dans une séquence et en collectant les valeurs résultantes dans une séquence de résultats. Dans Python, une liste en compréhension est une expression qui effectue un tel calcul :
>>> odds = [1, 3, 5, 7, 9]
>>> [x+1 for x in odds]
[2, 4, 6, 8, 10]Le mot-clé for utilisé ci-dessus ne fait pas partie d'une boucle for, mais fait partie d'une liste en compréhension, car il se trouve entre crochets. La sous-expression x+1 est évaluée avec x lié à chaque élément de la liste odds des chiffres impairs à tour de rôle, et les valeurs résultantes sont collectées dans une liste.
Une autre opération de traitement de séquence commune consiste à sélectionner un sous-ensemble de valeurs qui satisfont certaines conditions. Les listes en compréhension peuvent également exprimer ce modèle, par exemple en sélectionnant tous les éléments de la liste odds qui sont des diviseurs de 25 .
>>> [x for x in odds if 25 % x == 0]
[1, 5]La forme générale d'une liste en compréhension est la suivante :
Pour évaluer une liste en compréhension, Python évalue la <sequence expression>, qui doit renvoyer une valeur itérative. Ensuite, pour chaque élément de la séquence, la valeur de l'élément est liée à <name>, l'expression <filter expression> est évaluée, et si elle donne une valeur réelle, l'expression <map expression> est évaluée. Les valeurs produites par <map expression> sont collectées dans une liste.
Un troisième motif commun dans le traitement de séquences est d'agréger toutes les valeurs d'une séquence en une seule valeur. Les fonctions intégrées sum, min et max sont autant d'exemples de fonctions d'agrégation.
En combinant les possibilités d'évaluation d'une expression pour chaque élément d'une liste, de sélection d'un sous-ensemble d'éléments et d'agrégation d'éléments, nous pouvons résoudre de nombreux problèmes en utilisant une approche de traitement de séquence.
Un nombre parfait est un nombre entier positif égal à la somme de ses diviseurs. Les diviseurs de n sont des nombres entiers positifs inférieurs à n qui divisent n sans reste. La liste des diviseurs de n peut se construire à l'aide d'une liste en compréhension.
>>> def divisors(n):
return [1] + [x for x in range(2, n) if n % x == 0]
>>> divisors(4)
[1, 2]
>>> divisors(12)
[1, 2, 3, 4, 6]En utilisant divisors, nous pouvons calculer tous les nombres parfaits de 1 à 1000 avec une autre liste en compréhension. (À noter que 1 est généralement considéré comme un nombre parfait, mais il ne passe pas le test avec notre définition de divisors.)
Nous pouvons réutiliser notre définition de divisors pour résoudre un autre problème : trouver le périmètre minimum d'un rectangle ayant des longueurs de côtés entières, étant donné sa superficie. La superficie d'un rectangle est le produit de sa hauteur par sa largeur. Par conséquent, étant donné la superficie et la hauteur, nous pouvons calculer la largeur. Nous pouvons affirmer que la largeur et la hauteur sont des diviseurs de la superficie pour que les longueurs des côtés soient des nombres entiers.
>>> def width(area, height):
assert area % height == 0
return area // heightLe périmètre d'un rectangle est la somme de la longueur de ses côtés :
>>> def perimeter(width, height):
return 2 * width + 2 * heightLa hauteur d'un rectangle ayant des longueurs de côté entières doit être un diviseur de sa superficie. Nous pouvons calculer le périmètre minimum en considérant toutes les hauteurs possibles :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
>>> def minimum_perimeter(area):
heights = divisors(area)
perimeters = [perimeter(width(area, h), h) for h in heights]
return min(perimeters)
>>> area = 80
>>> width(area, 5)
16
>>> perimeter(16, 5)
42
>>> perimeter(10, 8)
36
>>> minimum_perimeter(area)
36
>>> [minimum_perimeter(n) for n in range(1, 10)]
[4, 6, 8, 8, 12, 10, 16, 12, 12]
Fonctions d'ordre supérieur. Les motifs communs que nous avons observés dans le traitement des séquences peuvent s'exprimer à l'aide de fonctions d'ordre supérieur. D'abord, l'évaluation d'une expression pour chaque élément dans une séquence peut se faire en appliquant une fonction à chaque élément :
>>> def apply_to_all(map_fn, s):
return [map_fn(x) for x in s]Il est possible de filtrer les éléments d'une liste pour lesquels une expression est vraie en appliquant une fonction à chaque élément.
>>> def keep_if(filter_fn, s):
return [x for x in s if filter_fn(x)]Enfin, on peut réaliser de nombreuses formes d'agrégation en appliquant répétitivement une fonction de deux arguments à la valeur réduite jusqu'à présent (reduced) et chaque élément à tour de rôle.
2.
3.
4.
5.
>>> def reduce(reduce_fn, s, initial):
reduced = initial
for x in s:
reduced = reduce_fn(reduced, x)
return reduced
Par exemple, reduce peut être utilisé pour multiplier entre eux tous les éléments d'une séquence. En utilisant mul comme reduce_fn et 1 comme valeur initiale, reduce permet de calculer le produit d'une séquence de nombres.
>>> reduce(mul, [2, 4, 8], 1)
64Nous pouvons également trouver des nombres parfaits en utilisant ces fonctions d'ordre supérieur.
>>> def divisors_of(n):
divides_n = lambda x: n % x == 0
return [1] + keep_if(divides_n, range(2, n))
>>> divisors_of(12)
[1, 2, 3, 4, 6]
>>> from operator import add
>>> def sum_of_divisors(n):
return reduce(add, divisors_of(n), 0)
>>> def perfect(n):
return sum_of_divisors(n) == n
>>> keep_if(perfect, range(1, 1000))
[1, 6, 28, 496]Noms conventionnels. Pour les informaticiens, une fonction comme apply_to_all s'appelle souvent map et la fonction keep_if s'appelle souvent filter. En Python, les fonctions intégrées map et filter sont des généralisations de ces fonctions qui ne renvoient pas des listes. Ces fonctions sont décrites dans un chapitre ultérieur. Les définitions ci-dessus sont équivalentes à l'application du constructeur de liste au résultat des fonctions intégrées map et filter :
>>> apply_to_all = lambda map_fn, s: list(map(map_fn, s))
>>> keep_if = lambda filter_fn, s: list(filter(filter_fn, s))La fonction reduce est définie dans le module functools de la bibliothèque standard Python. Dans cette version, l'argument initial est facultatif :
>>> from functools import reduce
>>> from operator import mul
>>> def product(s):
return reduce(mul, s)
>>> product([1, 2, 3, 4, 5])
120Il est plus fréquent en Python d'utiliser directement les listes en compréhension plutôt que des fonctions d'ordre supérieur, mais les deux approches du traitement de séquences sont largement utilisées.
3-4. Abstraction de séquence ▲
Nous avons introduit deux types de données natives qui satisfont l'abstraction des séquences : les listes et les plages. Tous deux satisfont les conditions avec lesquelles nous avons commencé cette section : longueur et sélection des éléments. Python possède deux autres comportements de types de séquence qui étendent l'abstraction de séquence.
Appartenance. Il est possible de tester si une valeur appartient à une séquence. Python a deux opérateurs in et not in qui renvoient True ou False selon que l'élément apparaît dans une séquence.
>>> digits
[1, 8, 2, 8]
>>> 2 in digits
True
>>> 1828 not in digits
TrueTranche. Les séquences contiennent des séquences plus petites en elles. Une tranche (slice) d'une séquence est une suite quelconque de valeurs contiguës de la séquence d'origine, désignée par une paire d'entiers. Comme pour le constructeur range, le premier entier indique l'indice de départ de la tranche et le second désigne l'élément suivant le dernier élément de la tranche.
En Python, les tranches de séquences s'expriment de manière analogue à la sélection des éléments, en utilisant des crochets. Un caractère deux-points sépare les indices de départ et de fin. Toute limite qui est omise est supposée être une valeur extrême : 0 pour l'index de départ et la longueur de la séquence pour l'indice de fin.
>>> digits
[1, 8, 2, 8]
>>> digits[0:2]
[1, 8]
>>> digits[1:]
[8, 2, 8]Il est également possible d'utiliser des tranches sur les branches d'un arbre. Par exemple, nous voudrions peut-être placer une restriction sur le nombre de branches d'un arbre. Un arbre binaire est (récursivement) soit une feuille, soit une séquence d'au plus deux arbres binaires. Il est assez fréquent de vouloir binariser un arbre, c'est-à-dire calculer un arbre binaire à partir d'un arbre de départ en regroupant des branches adjacentes.
>>> def right_binarize(tree):
"""Construct a right-branching binary tree."""
if is_leaf(tree):
return tree
if len(tree) > 2:
tree = [tree[0], tree[1:]]
return [right_binarize(b) for b in tree]
>>> right_binarize([1, 2, 3, 4, 5, 6, 7])
[1, [2, [3, [4, [5, [6, 7]]]]]]L'énumération de ces comportements supplémentaires de l'abstraction séquence Python nous donne l'occasion de réfléchir à ce qui constitue une abstraction de données utile en général. La richesse d'une abstraction (c'est-à-dire le nombre de comportements qu'elle supporte) a des conséquences. Pour les utilisateurs d'une abstraction, des comportements supplémentaires peuvent être utiles. D'un autre côté, satisfaire toutes les exigences d'une abstraction riche avec un nouveau type de données peut être difficile. Une autre conséquence négative des abstractions riches est qu'elles sont plus longues à apprendre pour les utilisateurs.
Les séquences sont une abstraction riche parce qu'elles sont si omniprésentes en informatique que l'apprentissage de certains comportements complexes est justifié. En général, la plupart des abstractions définies par l'utilisateur doivent être gardées aussi simples que possible.
Lectures complémentaires. La syntaxe d'utilisation des tranches admet une grande variété de cas particuliers, tels que les valeurs initiales négatives, les valeurs de fin et le pas des valeurs intermédiaires. On pourra trouver une description complète dans la documentation officielle de Python 3. Voir aussi le chapitre sur les listes du livre Apprendre à programmer avec Python 3 de Gérard Swinnen disponible sur ce site. Dans ce chapitre, nous utiliserons uniquement les fonctions de base décrites ci-dessus.
3-5. Chaînes de caractères ▲
Les valeurs textuelles sont peut-être plus fondamentales encore en informatique que les nombres. À titre d'exemple, les programmes Python sont écrits et stockés sous forme de texte. Le type de données natif pour le texte en Python s'appelle chaîne de caractères (string), ou souvent simplement chaîne (quand le contexte est clair), et correspond au constructeur str.
Il y a beaucoup de choses à dire sur la façon dont les chaînes sont représentées, exprimées et manipulées dans Python. Les chaînes sont un autre exemple d'une abstraction riche exigeant de la part du programmeur un investissement substantiel pour les maîtriser. Cette section sert d'introduction condensée aux comportements essentiels des chaînes.
Les chaînes littérales peuvent exprimer un texte arbitraire, et sont placées entre des apostrophes (ou guillemets simples) ou entre guillemets (doubles).
>>> 'I am string!'
'I am string!'
>>> "I've got an apostrophe"
"I've got an apostrophe"
>>> '您好'
'您好'Nous avons déjà vu des chaînes dans notre code, sous la forme de docstrings, dans les appels à la fonction print et en tant que messages d'erreur dans les instructions de type assert.
Les chaînes satisfont les deux conditions de base d'une séquence que nous avons introduites au début de cette section : elles ont une longueur et elles permettent la sélection d'éléments.
>>> city = 'Berkeley'
>>> len(city)
8
>>> city[3]
'k'Les éléments d'une chaîne sont eux-mêmes des chaînes qui n'ont qu'un seul caractère. Un caractère est une seule lettre de l'alphabet, un signe de ponctuation ou autre symbole. Contrairement à beaucoup d'autres langages de programmation, Python n'a pas de type caractère distinct ; tout texte est une chaîne, et les chaînes qui représentent des caractères uniques ont une longueur de 1.
Comme les listes, les chaînes peuvent également être combinées par addition et multiplication.
>>> 'Berkeley' + ', CA'
'Berkeley, CA'
>>> 'Shabu ' * 2
'Shabu Shabu 'Appartenance. En Python, le comportement des chaînes diverge d'autres types de séquences. L'abstraction de chaîne n'est pas entièrement conforme à l'abstraction de séquence que nous avons décrite pour les listes et les intervalles. En particulier, l'opérateur d'appartenance s'applique aux chaînes, mais a un comportement totalement différent que lorsqu'il est appliqué à des séquences. Il reconnaît des sous-chaînes et non des éléments individuels.
>>> 'here' in "Where's Waldo?"
TrueChaînes littérales multilignes. Les chaînes ne se limitent pas forcément à une seule ligne. Des guillemets triples permettent de créer des chaînes littérales qui comportent plusieurs lignes. Nous avons déjà utilisé ces guillemets triples pour les docstrings.
>>> """The Zen of Python
claims, Readability counts.
Read more: import this."""
'The Zen of Python\nclaims, "Readability counts."\nRead more: import this.'Dans le résultat affiché ci-dessus, le \n (« barre oblique inverse et lettre n ») est un élément unique qui représente une nouvelle ligne. Bien qu'il apparaisse comme deux caractères (barre oblique inverse et « n »), il est considéré comme un seul caractère dans la détermination de la longueur d'une chaîne et pour la sélection d'un élément.
Coercition de chaîne. Une chaîne peut être créée à partir d'un objet Python quelconque en appelant la fonction str avec un objet comme argument. Cette fonctionnalité des chaînes est utile pour la construction de chaînes descriptives à partir d'objets de différents types.
Lectures complémentaires. L'encodage de texte dans les ordinateurs est un sujet complexe. Dans ce chapitre, nous résumons la façon dont les chaînes sont représentées et omettons de nombreux détails. Toutefois, pour de nombreuses applications, les informations particulières sur la façon dont les chaînes sont encodées par les ordinateurs sont des connaissances essentielles. On pourra trouver une description complète dans la documentation officielle de Python 3. Voir aussi la section sur les chaînes de caractères du livre Apprendre à programmer avec Python 3 de Gérard Swinnen ou le chapitre sur les chaînes de caractères du livre Pensez en Python d'Allen B. Downey également disponible en français sur ce site.
3-6. Les arbres ▲
Notre capacité à utiliser des listes comme éléments d'autres listes fournit un nouveau moyen de combinaison dans notre langage de programmation. Cette capacité s'appelle une propriété de fermeture d'un type de données. En général, une méthode pour combiner des valeurs de données a une propriété de fermeture si le résultat de la combinaison peut être combiné à son tour en utilisant la même méthode. La fermeture est la clé de la puissance expressive dans toutes les formes de combinaison, car elle nous permet de créer des structures hiérarchiques – des structures constituées de pièces, elles-mêmes composées de pièces, et ainsi de suite.
Nous pouvons visualiser les listes dans les diagrammes d'environnement à l'aide de la notation boîte-et-pointeur. Une liste est représentée sous la forme de boîtes adjacentes contenant les éléments de la liste. Les valeurs natives telles que les nombres, les chaînes, les valeurs booléennes et None apparaissent dans une boîte élémentaire. Les valeurs composites, telles que les valeurs de fonction et d'autres listes, sont indiquées par une flèche.
3-7. Les listes chaînées ▲
Jusqu'à présent, nous n'avons utilisé que des types natifs pour représenter des séquences. Cependant, nous pouvons également développer des représentations séquentielles qui ne sont pas intégrées dans Python. Une liste chaînée est une représentation commune d'une séquence construite à partir de paires imbriquées. Le diagramme d'environnement ci-dessous illustre la représentation sous la forme d'une liste chaînée d'une séquence de quatre éléments contenant les chiffres 1, 2, 3 et 4.
Une liste chaînée est une paire contenant le premier élément de la séquence (dans ce cas 1) et le reste de la séquence (dans ce cas une représentation de 2, 3, 4). Le deuxième élément est également une liste chaînée. Le reste de la liste la plus imbriquée contenant seulement 4 est 'empty', une valeur qui représente une liste chaînée vide.
Les listes chaînées ont une structure récursive : le reste d'une liste chaînée est une liste chaînée ou 'empty'. Nous pouvons définir une représentation abstraite des données pour valider, construire et sélectionner les composants des listes chaînées.
>>> empty = 'empty'
>>> def is_link(s):
"""s is a linked list if it is empty or a (first, rest) pair."""
return s == empty or (len(s) == 2 and is_link(s[1]))
>>> def link(first, rest):
"""Construct a linked list from its first element and the rest."""
assert is_link(rest), "rest must be a linked list."
return [first, rest]
>>> def first(s):
"""Return the first element of a linked list s."""
assert is_link(s), "first only applies to linked lists."
assert s != empty, "empty linked list has no first element."
return s[0]
>>> def rest(s):
"""Return the rest of the elements of a linked list s."""
assert is_link(s), "rest only applies to linked lists."
assert s != empty, "empty linked list has no rest."
return s[1]Ci-dessus, la fonction link est un constructeur, et les fonctions first et rest sont des sélecteurs pour une représentation de données abstraites des listes chaînées. La condition de comportement d'une liste chaînée est que, comme pour une paire, son constructeur et ses sélecteurs sont des fonctions inverses.
- Si une liste chaînée s a été construite à partir du premier élément f et de la liste chaînée r, alors l'appel first(s) retourne f, et l'appel rest(s) renvoie r.
Nous pouvons utiliser le constructeur et les sélecteurs pour manipuler les listes chaînées.
>>> four = link(1, link(2, link(3, link(4, empty))))
>>> first(four)
1
>>> rest(four)
[2, [3, [4, 'empty']]]Notre implémentation de ce type de données abstraites utilise des paires qui sont des valeurs de type list à deux éléments. Il convient de noter que nous avons également pu construire des paires en utilisant des fonctions, et nous pouvons implémenter des listes chaînées à l'aide de toutes les paires, donc nous pourrions implémenter des listes chaînées en utilisant uniquement des fonctions.
Une liste chaînée peut stocker une séquence de valeurs dans l'ordre, mais nous n'avons pas encore montré qu'elle satisfait l'abstraction de la séquence. En utilisant la représentation abstraite des données que nous avons définie, nous pouvons instaurer les deux comportements qui caractérisent une séquence : la longueur et la sélection d'élément.
>>> def len_link(s):
"""Return the length of linked list s."""
length = 0
while s != empty:
s, length = rest(s), length + 1
return length
>>> def getitem_link(s, i):
"""Return the element at index i of linked list s."""
while i > 0:
s, i = rest(s), i - 1
return first(s)Maintenant, nous pouvons manipuler une liste chaînée comme une séquence utilisant ces fonctions. (Nous ne pouvons pas encore utiliser la fonction len intégrée, la syntaxe de sélection d'élément ni instruction for, mais nous serons bientôt en mesure de le faire.)
>>> len_link(four)
4
>>> getitem_link(four, 1)
2La série de diagrammes d'environnement ci-dessous illustre le processus itératif par lequel getitem_link trouve l'élément 2 à l'indice 1 dans une liste chaînée. Ci-dessous, nous avons défini la liste chaînée four en utilisant les primitives Python pour simplifier les diagrammes. Ce choix de mise en œuvre enfreint une barrière d'abstraction, mais nous permet d'inspecter le processus de calcul plus facilement pour cet exemple.
1 def first(s):
2 return s[0]
3 def rest(s):
4 return s[1]
5
6 def getitem_link(s, i):
7 while i > 0:
8 s, i = rest(s), i - 1
9 return first(s)
10
11 four = [1, [2, [3, [4, 'empty']]]]
12 getitem_link(four, 1)Au départ, la fonction getitem_link est appelée et crée un cadre local.
1 def first(s):
2 return s[0]
3 def rest(s):
4 return s[1]
5
6 def getitem_link(s, i):
7 while i > 0:
8 s, i = rest(s), i - 1
9 return first(s)
10
11 four = [1, [2, [3, [4, 'empty']]]]
12 getitem_link(four, 1)L'expression dans l'entête de l'instruction while s'évalue à True, ce qui entraîne l'exécution de l'instruction d'affectation dans le corps du while. La fonction rest renvoie la sous-liste à partir de 2.
1 def first(s):
2 return s[0]
3 def rest(s):
4 return s[1]
5
6 def getitem_link(s, i):
7 while i > 0:
8 s, i = rest(s), i - 1
9 return first(s)
10
11 four = [1, [2, [3, [4, 'empty']]]]
12 getitem_link(four, 1)Ensuite, le nom local s sera mis à jour pour désigner la sous-liste qui commence au deuxième élément de la liste d'origine. L'évaluation de l'expression dans l'en-tête de l'instruction while renvoie maintenant une valeur fausse, et Python sort de la boucle while et évalue l'expression dans l'instruction de retour de la dernière ligne de getitem_link.
1 def first(s):
2 return s[0]
3 def rest(s):
4 return s[1]
5
6 def getitem_link(s, i):
7 while i > 0:
8 s, i = rest(s), i - 1
9 return first(s)
10
11 four = [1, [2, [3, [4, 'empty']]]]
12 getitem_link(four, 1)Ce diagramme d'environnement final montre la trame locale pour l'appel de first, qui contient le nom s lié à cette même sous-liste. La fonction first sélectionne la valeur 2 et la renvoie ; cette valeur sera également retournée par getitem_link.
Cet exemple illustre un modèle commun de calcul avec des listes chaînées : chaque étape d'une itération traite un suffixe de plus en plus court de la liste d'origine. Ce traitement incrémental de recherche de la longueur et des éléments d'une liste chaînée prend du temps à calculer. Les types de séquence intégrés de Python sont implémentés d'une manière différente qui n'a pas ce coût élevé pour calculer la longueur d'une séquence ou récupérer de ses éléments. Les détails de cette représentation dépassent le périmètre de ce texte.
Manipulation récursive. Les fonctions liens len_link et getitem_link sont itératifs. Ils éliminent chaque couche de paire imbriquée jusqu'à la fin de la liste (dans len_link) ou jusqu'à ce que l'élément désiré (dans getitem_link) soit atteint. Nous pouvons également implémenter le calcul de la longueur et la sélection des éléments en utilisant la récursivité :
>>> def len_link_recursive(s):
"""Return the length of a linked list s."""
if s == empty:
return 0
return 1 + len_link_recursive(rest(s))
>>> def getitem_link_recursive(s, i):
"""Return the element at index i of linked list s."""
if i == 0:
return first(s)
return getitem_link_recursive(rest(s), i - 1)
>>> len_link_recursive(four)
4
>>> getitem_link_recursive(four, 1)
2Ces implémentations récursives suivent la chaîne de paires jusqu'à la fin de la liste (en len_link_recursive) ou jusqu'à ce que l'élément recherché (en getitem_link_recursive) soit atteint.
La récursivité est également utile pour transformer et combiner des listes chaînées :
>>> def extend_link(s, t):
"""Return a list with the elements of s followed by those of t."""
assert is_link(s) and is_link(t)
if s == empty:
return t
else:
return link(first(s), extend_link(rest(s), t))
>>> extend_link(four, four)
[1, [2, [3, [4, [1, [2, [3, [4, 'empty']]]]]]]]
>>> def apply_to_all_link(f, s):
"""Apply f to each element of s."""
assert is_link(s)
if s == empty:
return s
else:
return link(f(first(s)), apply_to_all_link(f, rest(s)))
>>> apply_to_all_link(lambda x: x*x, four)
[1, [4, [9, [16, 'empty']]]]
>>> def keep_if_link(f, s):
"""Return a list with elements of s for which f(e) is true."""
assert is_link(s)
if s == empty:
return s
else:
kept = keep_if_link(f, rest(s))
if f(first(s)):
return link(first(s), kept)
else:
return kept
>>> keep_if_link(lambda x: x%2 == 0, four)
[2, [4, 'empty']]
>>> def join_link(s, separator):
"""Return a string of all elements in s separated by separator."""
if s == empty:
return ""
elif rest(s) == empty:
return str(first(s))
else:
return str(first(s)) + separator + join_link(rest(s), separator)
>>> join_link(four, ", ")
'1, 2, 3, 4'Construction récursive. Les listes chaînées sont particulièrement utiles lors de la construction progressive de séquences, une situation qui survient souvent dans les calculs récursifs.
La fonction count_partitions fonction du premier chapitre comptait le nombre de façons de partitionner un nombre entier n en utilisant des parties jusqu'à la taille m par l'intermédiaire d'un processus récursif sur un arbre. Avec des séquences, on peut également énumérer ces partitions explicitement en employant un processus similaire.
Nous suivons la même analyse récursive du problème que nous avons faite tout en comptant : Le partitionnement n utilisant des entiers jusqu'à m implique soit :
- le partitionnement n-m en utilisant des nombres entiers allant jusqu'à m, soit
- le partitionnement n en utilisant des nombres entiers allant jusqu'à m-1.
Pour les cas de base, nous constatons que 0 a une partition vide, et qu'il est impossible de partitionner un nombre entier négatif ou d'utiliser des parties plus petites que 1.
>>> def partitions(n, m):
"""Return a linked list of partitions of n using parts of up to m.
Each partition is represented as a linked list.
"""
if n == 0:
return link(empty, empty) # A list containing the empty partition
elif n < 0 or m == 0:
return empty
else:
using_m = partitions(n-m, m)
with_m = apply_to_all_link(lambda s: link(m, s), using_m)
without_m = partitions(n, m-1)
return extend_link(with_m, without_m)Dans cette version récursive, on construit deux sous-listes de partitions. La première utilise m, donc on préfixe m à chaque élément du résultat using_m pour former with_m.
Le résultat de la fonction partitions est très imbriqué : une liste chaînée de listes chaînées, et chaque liste chaînée est représentée sous forme de paires imbriquées qui sont de type list. En utilisant join_link avec des séparateurs appropriés, on peut afficher les partitions d'une manière facile à lire pour un humain.
>>> def print_partitions(n, m):
lists = partitions(n, m)
strings = apply_to_all_link(lambda s: join_link(s, " + "), lists)
print(join_link(strings, "\n"))
>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 14. Données mutables ▲
Nous avons vu comment l'abstraction est essentielle pour nous aider à faire face à la complexité des grands systèmes. Une programmation efficace exige également des principes organisationnels qui peuvent nous guider dans la conception globale d'un programme. En particulier, nous avons besoin de stratégies pour nous aider à structurer les grands systèmes en sorte de les rendre modulaires, ce qui signifie qu'ils se divisent naturellement en des éléments cohérents qui peuvent être développés et maintenus séparément.
Une technique puissante pour créer des programmes modulaires est d'incorporer des données qui peuvent changer d'état au fil du temps. De cette façon, un seul objet de données peut représenter quelque chose qui évolue indépendamment du reste du programme. Le comportement d'un objet changeant peut être influencé par son histoire, tout comme une entité dans le monde. L'ajout d'état aux données est un ingrédient central d'un paradigme appelé programmation orientée objet.
4-1. La métaphore de l'objet ▲
Au début de ce texte, nous avons distingué les fonctions et les données : les fonctions appliquent des opérations et les données sont ce sur quoi ces opérations sont appliquées. Lorsque nous avons inclus des fonctions parmi nos données, nous avons reconnu que les données peuvent également avoir un comportement. Les fonctions peuvent être manipulées en tant que données, mais peuvent également être appelées à effectuer des calculs.
Les objets combinent les valeurs de données à un comportement. Les objets représentent des informations, mais se comportent aussi comme les choses qu'ils représentent. La logique de la façon dont un objet interagit avec d'autres objets est regroupée avec les informations qui encodent la valeur de l'objet. Lorsqu'un objet est imprimé, il sait comment se représenter dans du texte. Si un objet est un assemblage de composants, il sait comment révéler ces composants à la demande. Les objets sont à la fois des informations et des processus, regroupés pour représenter les propriétés, les interactions et les comportements de choses complexes.
Le comportement de l'objet est implémenté en Python à travers une syntaxe d'objet spécialisée et une terminologie associée, que nous pouvons introduire avec un exemple. Une date est une sorte d'objet.
>>> from datetime import dateLe nom date est lié à une classe. Comme nous l'avons vu, une classe représente une sorte de valeur. Les dates individuelles sont appelées instances de cette classe. Les instances peuvent être construites en appelant la classe sur les arguments qui caractérisent l'instance.
>>> tues = date(2014, 5, 13)L'objet tues (début du mot anglais signifiant mardi) a été construit à partir de nombres natifs, mais il se comporte comme une date. Par exemple, le soustraire d'une autre date donnera une différence de temps ou durée que nous pouvons imprimer.
>>> print(date(2014, 5, 19) - tues)
6 days, 0:00:00Les objets ont des attributs, qui sont des valeurs nommées faisant partie de l'objet. En Python, comme dans beaucoup d'autres langages de programmation, nous utilisons une notation dite pointée pour désigner l'attribut d'un objet.
<expression> . <name>Ci-dessus, <expression> s'évalue à un objet et <name> est le nom d'un attribut de cet objet.
Contrairement aux noms que nous avons considérés jusqu'ici, ces noms d'attributs ne sont pas disponibles dans l'environnement général. Au lieu de cela, les noms d'attributs sont particuliers à l'instance d'objet précédant le point.
>>> tues.year
2014Les objets ont également des méthodes, qui sont des attributs dont la valeur est une fonction. Nous disons métaphoriquement que l'objet « sait » comment exécuter ces méthodes. Par construction, les méthodes sont des fonctions qui calculent leurs résultats à partir à la fois de leurs arguments et de l'objet qui les invoque. Par exemple, la méthode strftime (le nom d'une fonction classique censée renvoyer une chaîne de caractères représentant une date) de tues prend un seul argument qui spécifie comment afficher une date (par exemple, %A signifie que le jour de la semaine doit être inséré en entier dans la chaîne).
>>> tues.strftime('%A, %B %d')
'Tuesday, May 13'Le calcul de la valeur de retour de strftime nécessite deux valeurs en entrée : la chaîne qui décrit le format de sortie et les informations relatives à la date regroupées en tues. Cette méthode applique une logique spécifique à la date pour générer ce résultat. Nous n'avons jamais spécifié que le 13 mai 2014 tombait un mardi, mais connaître le jour de semaine fait partie de ce que cela signifie d'être une date. En regroupant le comportement et l'information ensemble, cet objet Python nous offre une abstraction convaincante et autonome d'une date.
Les dates sont des objets, mais les nombres, les chaînes, les listes et les plages sont tous des objets. Non seulement ils représentent des valeurs, mais ils se comportent aussi de manière à respecter les valeurs qu'ils représentent. Ils ont également des attributs et des méthodes. Par exemple, les chaînes de caractères ont un ensemble de méthodes qui facilitent le traitement du texte.
>>> '1234'.isnumeric()
True
>>> 'rOBERT dE nIRO'.swapcase()
'Robert De Niro'
>>> 'eyes'.upper().endswith('YES')
TrueEn fait, toutes les valeurs de Python sont des objets. C'est-à-dire que toutes les valeurs ont un comportement et des attributs. Ils agissent comme les valeurs qu'ils représentent.
4-2. Objets séquentiels ▲
Les instances de valeurs intégrées primitives telles que les nombres sont immuables. Les valeurs elles-mêmes ne peuvent pas changer au cours de l'exécution du programme. Les listes, en revanche, sont mutables.
Les objets mutables sont utilisés pour représenter des valeurs qui changent avec le temps. Une personne est la même personne d'un jour à l'autre, si elle vieillit, subit une coupe de cheveux ou change d'une manière ou d'une autre. De même, un objet peut avoir des propriétés changeantes en raison des opérations de mutation. Par exemple, il est possible de modifier le contenu d'une liste. La plupart des modifications sont effectuées en invoquant des méthodes sur des objets de liste.
Nous pouvons présenter de nombreuses opérations de modification de listes avec un exemple qui illustre l'historique (radicalement simplifié) des cartes à jouer. Les commentaires dans les exemples décrivent l'effet de chaque appel de méthode.
Les cartes à jouer ont été inventées en Chine, peut-être vers le 9e siècle. Un des premiers jeux avait trois couleurs (en anglais, suits) correspondant à des dénominations d'argent.
>>> chinese = ['coin', 'string', 'myriad'] # Liste littérale
>>> suits = chinese # Deux noms désignant la même listeQuand les cartes ont migré vers l'Europe (en passant peut-être par l’Égypte), seule la couleur des pièces (coins) est resté dans les jeux de cartes espagnols (oro).
>>> suits.pop() # Supprime et retourne l'élément final
'myriad'
>>> suits.remove('string') # Supprimele premier élément égal à l'argumentTrois autres couleurs ont été ajoutées (leurs nom et apparence ont évolué au fil du temps) :
>>> suits.append('cup') # Ajout d'un élément à la fin
>>> suits.extend(['sword', 'club']) # Ajout de tous les éléments d'une séquence à la finEt les Italiens ont renommé les épées :
>>> suits[2] = 'spade' # Remplace un élémentCe qui donne les couleurs du jeu de cartes italien traditionnel :
>>> suits
['coin', 'cup', 'spade', 'club']La variante française (dont les quatre couleurs sont pique, cœur, carreau et trèfle, soit dans le même ordre diamond, heart, spade et club en anglais), la plus communément utilisée aujourd'hui aux États-Unis et dans d'autres pays, modifie les deux premières couleurs :
>>> suits[0:2] = ['heart', 'diamond'] # Remplace une tranche
>>> suits
['heart', 'diamond', 'spade', 'club']Des méthodes existent également pour l'insertion, le tri et l'inversion de listes. Toutes ces opérations de mutation modifient la valeur de la liste. Elles ne créent pas de nouveaux objets de liste.
Partage et identité. Comme nous avons changé une seule liste, et non créé de nouvelles listes, l'objet lié au nom chinois a également changé, car il s'agit du même objet-liste qui était lié à suits !
>>> chinese # Comme "suits", ce nom correspond à la même liste modifiée
['heart', 'diamond', 'spade', 'club']Ce comportement est nouveau. Jusqu'à présent, si un nom n'apparaissait pas dans une instruction, sa valeur ne pouvait pas être affectée par cette instruction. Avec les données mutables, les méthodes appelées sur un seul nom peuvent affecter un autre nom en même temps.
Le diagramme d'environnement pour cet exemple montre comment la valeur liée à chinese est modifiée par des instructions affectant uniquement des suits. Parcourez chaque ligne de l'exemple suivant pour observer ces modifications.
1 chinese = ['coin', 'string', 'myriad']
2 suits = chinese
3 suits.pop()
4 suits.remove('string')
5 suits.append('cup')
6 suits.extend(['sword', 'club'])
7 suits[2] = 'spade'
8 suits[0:2] = ['heart', 'diamond']Les listes peuvent être copiées à l'aide du constructeur list. Dans ce cas, les modifications apportées à une liste n'affectent pas l'autre, à moins qu'elles ne partagent une structure commune.
>>> nest = list(suits) # Liaison imbriquée à une seconde liste ayant les mêmes éléments
>>> nest[0] = suits # Création d'une liste imbriquéeDans cet environnement, changer la liste référencée par suits affectera la liste imbriquée qui est le premier élément de nest, mais pas les autres éléments.
>>> suits.insert(2, 'Joker') # Insère un élément à l'indice 2 et décale le reste
>>> nest
[['heart', 'diamond', 'Joker', 'spade', 'club'], 'diamond', 'spade', 'club']De même, défaire cette modification dans le premier élément de nest impactera également suits.
>>> nest[0].pop(2)
'Joker'
>>> suits
['heart', 'diamond', 'spade', 'club']Exécuter cet exemple pas à pas révélera la représentation d'une liste imbriquée.
1 suits = ['heart', 'diamond', 'spade', 'club']
2 nest = list(suits)
3 nest[0] = suits
4 suits.insert(2, 'Joker')
5 joke = nest[0].pop(2)Comme deux listes peuvent avoir le même contenu mais être en fait des listes différentes, nous avons besoin d'un moyen pour vérifier si deux objets sont identiques. Python fournit deux opérateurs de comparaison d'identité, appelés is et is not, qui testent si deux expressions renvoient le même objet. Deux objets sont identiques s'ils ont actuellement la même valeur et si tout changement à l'un sera toujours reflété dans l'autre. L'identité est une condition plus forte que l'égalité.
>>> suits is nest[0]
True
>>> suits is ['heart', 'diamond', 'spade', 'club']
False
>>> suits == ['heart', 'diamond', 'spade', 'club']
TrueLes deux dernières comparaisons illustrent la différence entre les opérateurs is et ==. Le premier vérifie l'identité, tandis que le dernier vérifie l'égalité des contenus.
Listes en compréhension. Une liste en compréhension crée toujours une nouvelle liste. Par exemple, le module unicodedata stocke les noms officiels de chaque caractère dans l'alphabet Unicode. Nous pouvons rechercher les caractères correspondant aux noms, y compris ceux des couleurs de cartes.
>>> from unicodedata import lookup
>>> [lookup('WHITE ' + s.upper() + ' SUIT') for s in suits]
['♡', '♢', '♤', '♧']Cette liste résultante ne partage pas son contenu avec suits, et l'évaluation de la liste en compréhension ne modifie pas la liste suits.
Tuples. Un tuple, une instance du type tuple intégré, est une séquence immuable. Les tuples sont créés en utilisant un tuple littéral qui sépare les expressions des éléments par des virgules. Les parenthèses sont facultatives mais utilisées couramment dans la pratique. On peut stocker toutes sortes d'objets dans des tuples.
>>> 1, 2 + 3
(1, 5)
>>> ("the", 1, ("and", "only"))
('the', 1, ('and', 'only'))
>>> type( (10, 20) )
<class 'tuple'>Les tuples vides et à un seul élément ont une syntaxe littérale spéciale :
>>> () # 0 elements
()
>>> (10,) # 1 element
(10,)Comme les listes, les tuples ont une longueur finie et autorisent la sélection d'éléments. Ils ont également quelques méthodes qui sont également disponibles pour les listes, comme count et index :
>>> code = ("up", "up", "down", "down") + ("left", "right") * 2
>>> len(code)
8
>>> code[3]
'down'
>>> code.count("down")
2
>>> code.index("left")
4Cependant, les méthodes de manipulation du contenu d'une liste ne sont pas disponibles pour les tuples puisque les tuples sont immuables.
Bien qu'il soit impossible de modifier les éléments d'un tuple, il est possible de modifier la valeur d'un élément mutable contenu dans un tuple.
1 nest = (10, 20, [30, 40])
2 nest[2].pop()Les tuples sont utilisés implicitement dans les affectations multiples. Une affectation de deux valeurs à deux noms crée un tuple à deux éléments puis dépaquette les éléments.
4-3. Dictionnaires ▲
Les dictionnaires sont le type de données intégré de Python pour stocker et manipuler les relations de correspondance. Un dictionnaire contient des paires clef-valeur, dans lesquelles les clefs et les valeurs sont des objets. Le but d'un dictionnaire est de fournir une abstraction pour stocker et récupérer des valeurs qui sont indexées non par des entiers consécutifs, mais par des clefs descriptives.
Les clefs sont souvent des chaînes de caractères, car les chaînes sont notre représentation conventionnelle des noms de choses. Ce dictionnaire littéral donne les valeurs de différents chiffres romains.
>>> numerals = {'I': 1.0, 'V': 5, 'X': 10}La recherche de valeurs par leurs clefs utilise l'opérateur de sélection d'élément que nous avons précédemment employé pour des séquences :
>>> numerals['X']
10Un dictionnaire peut avoir au plus une valeur pour chaque clef. L'ajout de nouvelles paires de clefs-valeurs et la modification de la valeur existante d'une clé peuvent s'effectuer par des instructions d'affectation :
>>> numerals['I'] = 1
>>> numerals['L'] = 50
>>> numerals
{'I': 1, 'X': 10, 'L': 50, 'V': 5}Notez que 'L' n'a pas été ajouté à la fin de la sortie ci-dessus (mais avant). Les dictionnaires sont des collections non ordonnées de paires clef-valeur. Lorsque nous imprimons un dictionnaire, les clés et les valeurs sont rendues dans un certain ordre, mais en tant qu'utilisateurs du langage, nous ne pouvons pas prédire ce que sera cet ordre. L'ordre peut changer si nous lançons plusieurs fois le même programme.
Les dictionnaires peuvent également apparaître dans des diagrammes d'environnement.
1 numerals = {'I': 1, 'V': 5, 'X': 10}
2 numerals['L'] = 50Le type Dictionary prend également en charge diverses méthodes d'itération sur le contenu du dictionnaire dans son ensemble. Les méthodes keys, values et items renvoient toutes les valeurs itérables.
>>> sum(numerals.values())
66Une liste de paires clé-valeur peut être convertie en un dictionnaire en appelant la fonction constructeur dict.
>>> dict([(3, 9), (4, 16), (5, 25)])
{3: 9, 4: 16, 5: 25}Les dictionnaires ont certaines restrictions :
- Une clé d'un dictionnaire ne peut pas être ou contenir une valeur mutable.
- Il peut y avoir au plus une valeur pour une clé donnée.
Cette première restriction est liée à la mise en œuvre sous-jacente des dictionnaires dans Python. Ce texte ne couvrira pas les détails de cette implémentation. Intuitivement, considérez que la clé indique à Python où trouver cette paire clé-valeur dans la mémoire ; si la clé change, l'emplacement de la paire peut être perdu. On utilise assez couramment des tuples comme clés dans les dictionnaires, parce que les listes (qui sont mutables) ne peuvent pas servir de clés.
La deuxième restriction est une conséquence de l'abstraction du dictionnaire, qui est conçu pour stocker et récupérer des valeurs pour les clés. Nous ne pouvons que récupérer la valeur d'une clé que s'il existe au plus une seule valeur pour cette clé dans le dictionnaire.
Les dictionnaires offrent une méthode utile, get, qui renvoie soit la valeur correspondant à la clé, si la clé est présente, soit une valeur par défaut. Les arguments de get sont la clé et la valeur par défaut.
>>> numerals = {'I': 1, 'V': 5, 'X': 10}
>>> numerals.get('A', 0)
0
>>> numerals.get('V', 0)
5Les dictionnaires ont également une syntaxe de compréhension analogue à celle des listes. Une expression de clé et une expression de valeur sont séparées par deux points. L'évaluation d'un dictionnaire en compréhension crée un nouvel objet de type dictionnaire.
>>> {x: x*x for x in range(3,6)}
{3: 9, 4: 16, 5: 25}4-4. État local ▲
Les listes et les dictionnaires ont un état local : ce sont des valeurs changeantes qui ont des contenus particuliers à un moment quelconque de l'exécution d'un programme. Le mot « état » implique un processus évolutif dans lequel cet état peut changer.
Les fonctions peuvent également avoir un état local. Par exemple, définissons une fonction qui modélise le processus de retrait d'argent d'un compte bancaire. Nous allons créer une fonction de retrait appelée withdraw, qui prend comme argument un montant à retirer. S'il y a suffisamment d'argent dans le compte pour couvrir le retrait, withdraw renverra le solde du compte après le retrait. Sinon, withdraw renverra le message « Insufficient funds ». Par exemple, si nous démarrons avec un crédit de 100 € sur le compte, nous souhaitons obtenir la séquence suivante de valeurs de retour en appelant withdraw :
>>> withdraw(25)
75
>>> withdraw(25)
50
>>> withdraw(60)
'Insufficient funds'
>>> withdraw(15)
35Ci-dessus, l'expression withdraw(25), évaluée à deux reprises, renvoie des valeurs différentes. Ainsi, cette fonction définie par l'utilisateur n'est pas pure. L'appel de la fonction renvoie non seulement une valeur, mais a aussi pour effet secondaire de modifier en un certain sens la fonction, de sorte que l'appel suivant avec le même argument renvoie un résultat différent. Cet effet secondaire résulte du fait que withdraw modifie une liaison nom-valeur externe au cadre courant.
Pour que la fonction withdraw ait un sens, il faut qu'elle soit créée avec un solde de compte initial. La fonction make_withdraw est une fonction d'ordre supérieur qui prend un solde de départ comme argument. La fonction de withdraw est sa valeur de retour :
>>> withdraw = make_withdraw(100)Une implémentation de make_withdraw nécessite un nouveau type d'instruction : une instruction nonlocal. Lorsque nous appelons make_withdraw, nous lions le nom balance (solde) au nom du montant initial. Nous définissons et renvoyons une fonction locale, withdraw, qui met à jour et renvoie la valeur de balance lorsqu'elle est appelée.
>>> def make_withdraw(balance):
"""Return a withdraw function that draws down balance with each call."""
def withdraw(amount):
nonlocal balance # Declare the name "balance" nonlocal
if amount > balance:
return 'Insufficient funds'
balance = balance - amount # Re-bind the existing balance name
return balance
return withdrawLa déclaration nonlocal indique que chaque fois que nous modifions la liaison du nom balance, cette liaison est modifiée dans le premier cadre dans lequel balance est déjà lié. Rappelons que, sans l'instruction nonlocal, une instruction d'affectation lierait toujours un nom dans le premier cadre de l'environnement courant. L'instruction nonlocal indique que le nom apparaît quelque part dans l'environnement ailleurs que dans le premier cadre (local) ou dans le dernier cadre (global).
Les diagrammes d'environnement suivants illustrent les effets de plusieurs appels vers une fonction créée par make_withdraw.
1 def make_withdraw(balance):
2 def withdraw(amount):
3 nonlocal balance
4 if amount > balance:
5 return 'Insufficient funds'
6 balance = balance - amount
7 return balance
8 return withdraw
9
10 wd = make_withdraw(20)
11 wd(5)
12 wd(3)La première instruction def a l'effet habituel : elle crée une nouvelle fonction définie par l'utilisateur et lie le nom make_withdraw à cette fonction dans le cadre global. L'appel à make_withdraw plus bas crée et renvoie une fonction définie localement, withdraw. Le nom balance est lié au cadre parent de cette fonction. Il est essentiel de remarquer qu'il n'y aura que cette liaison unique pour le nom balance dans le reste de cet exemple.
Ensuite, nous évaluons une expression qui appelle cette fonction et la lie au nom wd, pour un montant de 5. Le corps de withdraw est exécuté dans un nouvel environnement qui étend l'environnement dans lequel la fonction withdraw a été définie. En traçant l'effet de l'évaluation du withdraw, on constate l'effet d'une déclaration nonlocal en Python : un nom en dehors du premier cadre local peut être modifié par une instruction d'affectation.
1 def make_withdraw(balance):
2 def withdraw(amount):
3 nonlocal balance
4 if amount > balance:
5 return 'Insufficient funds'
6 balance = balance - amount
7 return balance
8 return withdraw
9
10 wd = make_withdraw(20)
11 wd(5)
12 wd(3)La déclaration nonlocal modifie toutes les autres instructions d'affectation dans la définition de withdraw. Après avoir exécuté une déclaration nonlocal balance, toute instruction d'affectation avec balance à gauche du signe = ne liera pas balance dans le premier cadre de l'environnement actuel. Au lieu de cela, l'affectation trouvera le premier cadre dans lequel balance a déjà été défini et reliera le nom dans ce cadre. Si le nom balance n'était pas déjà lié à une valeur, l'instruction nonlocal produirait une erreur.
En raison de la modification de la liaison pour balance, nous avons également changé la fonction withdraw. La prochaine fois qu'on appellera cette fonction, le nom balance sera évalué à 15 au lieu de 20. Par conséquent, lorsque nous appelons withdraw une deuxième fois avec la valeur 3, nous voyons que sa valeur de retour est de 12 et non pas 17. La modification de balance lors du premier appel affecte le résultat du second appel.
1 def make_withdraw(balance):
2 def withdraw(amount):
3 nonlocal balance
4 if amount > balance:
5 return 'Insufficient funds'
6 balance = balance - amount
7 return balance
8 return withdraw
9
10 wd = make_withdraw(20)
11 wd(5)
12 wd(3)Le deuxième appel à withdraw crée un deuxième cadre local, comme d'habitude. Toutefois, les deux cadres withdraw ont le même parent. Autrement dit, ils étendent l'environnement de make_withdraw, qui contient la liaison de balance. Par conséquent, ils partagent cette liaison de nom particulière. L'appel de withdraw a pour effet secondaire de modifier l'environnement qui sera prolongé par les appels futurs à withdraw. La déclaration nonlocal permet à withdraw de modifier une liaison de nom dans le cadre de make_withdraw.
Depuis que nous avons commencé à rencontrer des instructions def imbriquées, nous avons observé qu'une fonction définie localement peut rechercher des noms en dehors de ses cadres locaux. Une déclaration nonlocal n'est pas nécessaire pour accéder à un nom non local. En revanche, c'est seulement après une déclaration nonlocal qu’une fonction peut modifier la liaison des noms dans ces cadres.
Guide pratique. En introduisant des déclarations nonlocal, nous avons créé deux rôles différents pour les déclarations d'affectation. Soit elles modifient des liaisons locales, soit elles modifient les liaisons non locales. En fait, les déclarations d'affectation avaient déjà un double rôle : elles pouvaient créer de nouvelles liaisons ou re-lier des noms existants. Une affectation peut aussi modifier le contenu de listes et de dictionnaires. Les nombreux rôles de l'affectation en Python peuvent obscurcir les effets de l'exécution d'une instruction d'affectation. C'est à vous, en tant que programmeur, de documenter votre code de manière claire pour que les effets d'une affectation soient bien compris par d'autres.
Particularités Python. Ce modèle d'affectation non locale est une caractéristique générale des langages de programmation ayant des fonctions d'ordre supérieur et une portée lexicale. La plupart de ces autres langues ne requièrent aucune déclaration nonlocal. Pour eux, l'affectation non locale est souvent le comportement par défaut des instructions d'affectation.
Python a également une restriction inhabituelle concernant la recherche de noms : dans le corps d'une fonction, toutes les instances d'un nom doivent se référer au même cadre. Par conséquent, Python ne peut pas rechercher la valeur d'un nom dans un cadre non local, puis lier ce même nom dans le cadre local, car le même nom serait accessible dans deux cadres différents dans la même fonction. Cette restriction permet à Python de précalculer quel cadre contient quel nom avant même d'exécuter le corps d'une fonction. Toute violation de cette restriction entraîne l'émission d'un message d'erreur pas très clair. Pour le montrer, reprenons l'exemple make_withdraw avec l'instruction nonlocal supprimée.
1 def make_withdraw(balance):
2 def withdraw(amount):
3 if amount > balance:
4 return 'Insufficient funds'
5 balance = balance - amount
6 return balance
7 return withdraw
8
9 wd = make_withdraw(20)
10 wd(5)Cela affiche l'erreur suivante :
UnboundLocalError: local variable 'balance' referenced before assignmentCette erreur UnboundLocalError apparaît parce que balance est affecté localement à la ligne 5, et Python suppose donc que toutes les références à balance doivent également apparaître dans le cadre local. Cette erreur se produit avant même que la ligne 5 ne soit exécutée, ce qui implique que Python a examiné la ligne 5 d'une certaine manière avant d'exécuter la ligne 3. Lorsque nous étudierons la conception de l'interpréteur, nous verrons qu'il est assez courant de précalculer des informations sur le corps d'une fonction avant de l'exécuter. Dans ce cas, le prétraitement de Python a restreint le cadre dans lequel balance pourrait apparaître, empêchant ainsi que ce nom puisse être trouvé. L'ajout d'une déclaration nonlocal corrige cette erreur. La déclaration nonlocal n'existait pas en Python 2.
4-5. Les avantages de l'affectation non locale▲
L'affectation non locale est une étape importante sur notre chemin vers la conception d'un programme comme une collection d'objets indépendants et autonomes, qui interagissent les uns avec les autres, mais dans lequel chacun gère son propre état interne.
En particulier, l'affectation non locale nous a permis de maintenir un état local à une fonction, mais qui évolue au fur et à mesure des appels successifs à cette fonction. Le solde balance associé à une fonction de retrait particulière est partagé entre tous les appels à cette fonction. Cependant, la liaison de ce solde associée à une instance de retrait est inaccessible au reste du programme. Seul wd est associé au cadre de make_withdraw dans lequel il a été défini. Si la fonction make_withdraw est appelée à nouveau, elle créera un cadre séparé avec une liaison distincte pour balance.
Nous pouvons étendre notre exemple pour illustrer ce point. Un deuxième appel à make_withdraw renvoie une deuxième fonction de retrait withdraw qui a un parent différent. Nous lions cette deuxième fonction au nom wd2 dans le cadre global.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
wd = make_withdraw(20)
wd2 = make_withdraw(7)
wd2(6)
wd(8)
Maintenant, nous voyons qu'il existe en fait deux liaisons pour le nom balance, dans deux cadres différents, et chaque fonction de withdraw a un parent différent. Le nom wd est lié à une fonction avec un solde de 20, tandis que wd2 est lié à une fonction différente avec un solde de 7.
L'appel wd2 modifie la liaison de son nom withdraw non local, mais n'affecte pas la fonction liée au nom withdraw. Un futur appel à wd n'est pas affecté par la modification du solde de wd2 ; son solde est encore de 20.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
wd = make_withdraw(20)
wd2 = make_withdraw(7)
wd2(6)
wd(8)
De cette façon, chaque instance de withdraw maintient son propre solde, mais cet état est inaccessible à toute autre fonction du programme. En regardant cette situation à un niveau supérieur, nous avons créé une abstraction d'un compte bancaire qui gère ses propres données internes, mais se comporte de manière à modéliser les comptes dans le monde : il évolue avec le temps en fonction de son historique des demandes de retrait.
4-6. Le coût de l'affectation non locale ▲
Notre modèle de calcul environnemental s'étend proprement pour expliquer les effets de l'affectation non locale. Toutefois, l'affectation non locale présente quelques nuances importantes dans la façon dont nous pensons aux noms et aux valeurs.
Auparavant, nos valeurs ne changeaient pas ; seuls nos noms et liens changeaient. Lorsque deux noms a et b étaient tous deux liés à la valeur 4, il n'importait pas qu'ils soient liés aux mêmes 4 ou à des 4 différents. Pour autant que l'on pût dire, il n'y avait qu'un seul objet 4 qui ne changeait jamais.
Cependant, les fonctions avec état ne se comportent pas de cette façon. Lorsque deux noms wd et wd2 sont liés à une fonction withdraw, il importe qu'ils soient liés à la même fonction ou à différentes instances de cette fonction. Considérons l'exemple suivant, qui s'oppose celui que nous venons d'analyser. Dans ce cas, appeler la fonction nommée par wd2 a changé la valeur de la fonction nommée par wd, car les deux noms se réfèrent à la même fonction.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
def make_withdraw(balance):
def withdraw(amount):
nonlocal balance
if amount > balance:
return 'Insufficient funds'
balance = balance - amount
return balance
return withdraw
wd = make_withdraw(12)
wd2 = wd
wd2(1)
wd(1)
Il n'est pas rare que deux noms se réfèrent à la même valeur dans le monde, et c'est également le cas dans nos programmes. Mais, quand les valeurs changent avec le temps, nous devons faire chercher très soigneusement à comprendre l'effet d'une modification sur d'autres noms qui pourraient se référer à ces valeurs.
La clef pour analyser correctement du code ayant une affectation non locale consiste à se rappeler que seuls les appels de fonctions peuvent introduire de nouveaux cadres. Les instructions d'affectation changent toujours les liens dans des cadres existants. Dans notre cas, à moins que make_withdraw ne soit appelé deux fois, il ne peut y avoir qu'une seule liaison pour le nom balance.
Identité et changement. Ces subtilités surviennent parce que, en introduisant des fonctions non-pures qui modifient l'environnement non local, nous avons changé la nature des expressions. Une expression qui ne contient que des appels de fonctions pures est dite référentiellement transparente : sa valeur ne change pas si nous substituons l'une de ses sous-expressions à la valeur de cette sous-expression.
Les opérations de re-liaison violent les conditions de transparence référentielle parce qu'elles font plus que renvoyer une valeur : elles modifient l'environnement. Lorsque nous introduisons une re-liaison quelconque, nous rencontrons un problème épistémologique épineux : que veut dire que deux valeurs sont les mêmes ? Dans notre modèle d'environnement de calcul, deux fonctions définies séparément ne sont pas les mêmes, car des modifications apportées à l'une peuvent ne pas affecter l'autre.
En général, tant que nous ne modifions jamais les objets de données, nous pouvons considérer un objet de données composé comme étant précisément la totalité de ses composants. Par exemple, un nombre rationnel est déterminé en donnant son numérateur et son dénominateur. Mais cette vue n'est plus valide en présence d'un changement, dans lequel un objet de données composé possède une « identité » différente des composants dont il est formé. Un compte bancaire est toujours « le même » compte bancaire même si nous changeons le solde en effectuant un retrait. À l'inverse, nous pourrions avoir deux comptes bancaires qui ont le même solde, mais sont des objets différents.
Malgré les complications qu'elle introduit, l'affectation non locale est un outil puissant pour créer des programmes modulaires. Les différentes parties d'un programme, qui correspondent à différents cadres d'environnement, peuvent évoluer séparément tout au long de l'exécution du programme. En outre, en utilisant des fonctions avec l'état local, nous sommes en mesure de mettre en œuvre des types de données mutables. En fait, nous pouvons mettre en place des types de données abstraits qui sont équivalents aux types internes list et dict introduits précédemment.
4-7. Implémentation de listes et de dictionnaires ▲
Le langage Python ne nous donne pas accès à la mise en œuvre des listes, mais seulement à l'abstraction et aux méthodes de mutation de séquences intégrées dans le langage. Pour comprendre comment une liste mutable pourrait être représentée à l'aide de fonctions avec l'état local, nous allons maintenant développer une implémentation d'une liste chaînée mutable.
Nous représenterons une liste chaînée mutable par une fonction qui a une liste chaînée dans son état local. Les listes doivent avoir une identité, comme toute valeur mutable. En particulier, nous ne pouvons pas utiliser None pour représenter une liste mutable vide, car deux listes vides ne sont pas des valeurs identiques (par exemple, ajouter un élément à l'une d'elles n'affecte pas à l'autre), mais None est None. D'un autre côté, deux fonctions différentes ayant toutes deux un état local empty permettront de distinguer deux listes vides.
Si une liste chaînée mutable est une fonction, quels arguments prend-elle ? La réponse illustre un modèle général de programmation : la fonction est une fonction de distribution (dispatch function) et ses arguments sont un message suivi des arguments supplémentaires pour paramétrer cette méthode. Ce message est une chaîne de caractères indiquant ce que la fonction doit faire. Les fonctions de distribution sont en réalité de nombreuses fonctions en une seule : le message détermine le comportement de la fonction, et les arguments supplémentaires sont utilisés dans ce comportement.
Notre liste mutable répondra à cinq messages différents : len, getitem, push_first, pop_first et str. Les deux premiers mettent en œuvre les comportements de l'abstraction de la séquence. Les deux suivants permettent d'ajouter ou de supprimer le premier élément de la liste. Le dernier message renvoie une représentation sous la forme de chaîne de caractères de l'ensemble de la liste chaînée.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
>>> def mutable_link():
"""Return a functional implementation of a mutable linked list."""
contents = empty
def dispatch(message, value=None):
nonlocal contents
if message == 'len':
return len_link(contents)
elif message == 'getitem':
return getitem_link(contents, value)
elif message == 'push_first':
contents = link(value, contents)
elif message == 'pop_first':
f = first(contents)
contents = rest(contents)
return f
elif message == 'str':
return join_link(contents, ", ")
return dispatch
Nous pouvons aussi ajouter une fonction pratique pour construire fonctionnellement une liste chaînée à partir de toute séquence du langage, en ajoutant simplement chaque élément dans l'ordre inverse.
2.
3.
4.
5.
6.
>>> def to_mutable_link(source):
"""Return a functional list with the same contents as source."""
s = mutable_link()
for element in reversed(source):
s('push_first', element)
return s
Dans la définition ci-dessus, la fonction reversed prend et retourne une valeur itérable ; c'est un autre exemple d'une fonction qui traite les séquences.
Nous pouvons maintenant construire des listes chaînées mutables mises en œuvre fonctionnellement. Notez que la liste chaînée elle-même est une fonction.
2.
3.
4.
5.
>>> s = to_mutable_link(suits)
>>> type(s)
<class 'function'>
>>> print(s('str'))
heart, diamond, spade, club
En outre, nous pouvons transmettre à la liste s des messages qui changent son contenu, par exemple enlever le premier élément.
2.
3.
4.
>>> s('pop_first')
'heart'
>>> print(s('str'))
diamond, spade, club
En principe, les opérations push_first et pop_first suffisent à apporter des modifications arbitraires à une liste. Nous pouvons toujours vider la liste entièrement et remplacer son ancien contenu par le résultat souhaité.
Le passage de messages. En y consacrant les efforts nécessaires, nous pourrions mettre en place les nombreuses opérations de mutation utiles de listes Python, comme extend et insert. Nous devrions faire un choix : nous pourrions les mettre en œuvre sous la forme de fonctions qui utilisent les messages existants pop_first et push_first pour faire tous ces changements. L'autre solution serait d'ajouter au corps de la fonction dispatch d' autres clauses elif qui s'appliqueraient chacune à un message donné (par exemple, extend) et effectueraient directement les changements voulus à contents.
Cette deuxième approche, qui encapsule la logique de toutes les opérations sur une donnée dans une fonction qui répond aux différents messages, est une discipline appelée passage de messages. Un programme qui utilise le passage de messages définit des fonctions de distribution, qui peuvent chacune avoir un état local, et organise le calcul en passant des « messages » comme premier argument à ces fonctions. Les messages sont des chaînes de caractères qui correspondent à des comportements particuliers.
Mise en œuvre de dictionnaires. Nous pouvons également mettre en œuvre une valeur avec un comportement similaire à un dictionnaire. Dans ce cas, nous utilisons une liste de paires clé-valeur pour stocker le contenu du dictionnaire. Chaque paire est une liste à deux éléments.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
>>> def dictionary():
"""Return a functional implementation of a dictionary."""
records = []
def getitem(key):
matches = [r for r in records if r[0] == key]
if len(matches) == 1:
key, value = matches[0]
return value
def setitem(key, value):
nonlocal records
non_matches = [r for r in records if r[0] != key]
records = non_matches + [[key, value]]
def dispatch(message, key=None, value=None):
if message == 'getitem':
return getitem(key)
elif message == 'setitem':
setitem(key, value)
return dispatch
Une nouvelle fois, nous utilisons la méthode de passage de messages pour organiser notre mise en œuvre. Nous mettons en place deux messages : getitem et setitem. Pour insérer une valeur pour une clef, nous filtrons tous les enregistrements existants avec la clef donnée, puis ajoutons l'enregistrement désiré. De cette façon, nous sommes assurés que chaque clef n'apparaît qu'une seule fois. Pour rechercher une valeur correspondant à une clef, nous filtrons l'enregistrement qui correspond à la clef donnée. Nous pouvons maintenant utiliser notre application pour stocker et récupérer des valeurs.
2.
3.
4.
5.
6.
7.
>>> d = dictionary()
>>> d('setitem', 3, 9)
>>> d('setitem', 4, 16)
>>> d('getitem', 3)
9
>>> d('getitem', 4)
16
Cette mise en œuvre d'un dictionnaire n'est pas optimisée pour la recherche rapide d'enregistrement, parce que chaque appel doit filtrer tous les enregistrements. Le type dictionnaire intégré dans Python est beaucoup plus efficace. La façon dont ce type est mis en œuvre en Python dépasse le cadre de ce texte.
4-8. Dictionnaires ou tables de distribution ▲
La fonction dispatch est une méthode générale de mise en œuvre d'une interface de passage de message pour les données abstraites. Pour mettre en œuvre l'envoi de messages, nous avons jusqu'ici utilisé des instructions conditionnelles pour comparer la chaîne de message à un ensemble fixe de messages connus.
Le type de données dictionnaire fournit une méthode générale pour rechercher une valeur correspondant à une clef. Au lieu d'utiliser des conditions de type if ... elif ... pour déterminer une action à effectuer, nous pouvons utiliser des dictionnaires avec des chaînes de caractères comme clefs.
Le type de données mutable account ci-dessous utilise un dictionnaire. Il a un constructeur account et un sélecteur check_balance, ainsi que des fonctions de deposit ou withdraw pour déposer ou retirer des fonds. De plus, l'état local du compte est stocké dans le dictionnaire, de même que les fonctions qui mettent en œuvre son comportement.
def account(initial_balance):
def deposit(amount):
dispatch['balance'] += amount
return dispatch['balance']
def withdraw(amount):
if amount > dispatch['balance']:
return 'Insufficient funds'
dispatch['balance'] -= amount
return dispatch['balance']
dispatch = {'deposit': deposit,
'withdraw': withdraw,
'balance': initial_balance}
return dispatch
def withdraw(account, amount):
return account['withdraw'](amount)
def deposit(account, amount):
return account['deposit'](amount)
def check_balance(account):
return account['balance']
a = account(20)
deposit(a, 5)
withdraw(a, 17)
check_balance(a)Le nom dispatch dans le corps du constructeur account est lié à un dictionnaire contenant les messages acceptés comme clefs par un compte. Le solde (balance) est un nombre, tandis que les messages de dépôt et de retrait sont liés à des fonctions. Ces fonctions ont accès au dictionnaire dispatch, et elles peuvent lire et modifier le solde. En stockant le solde dans le dictionnaire dispatch plutôt que dans le cadre account directement, nous évitons la nécessité de déclarations de type nonlocal dans deposit et withdraw.
Les opérateurs += et -= sont un raccourci en Python (et beaucoup d'autres langages de programmation) pour la lecture d'une valeur et la réaffectation. Les deux dernières lignes ci- dessous sont équivalentes.
>>> a = 2
>>> a = a + 1
>>> a += 14-9. Propagation de contraintes ▲
Les données mutables nous permettent non seulement de simuler des systèmes subissant des changements, mais aussi de construire de nouveaux types d'abstractions. Dans cet exemple étendu, nous combinons des affectations de type nonlocal, des listes et des dictionnaires pour construire un système basé sur des contraintes qui prend en charge des calculs dans plusieurs directions. Exprimer des programmes sous la forme de contraintes est une forme de programmation déclarative, dans laquelle un programmeur déclare la structure d'un problème à résoudre, mais fait abstraction des détails de la façon dont est calculée la solution au problème.
Les programmes informatiques sont traditionnellement organisés comme des calculs unidirectionnels, qui effectuent des opérations sur des arguments préspécifiés pour produire des résultats souhaités. D'un autre côté, nous voulons souvent modéliser des systèmes en termes de relations entre des quantités. Par exemple, nous avons considéré précédemment la loi des gaz parfaits, qui relie la pression (p), le volume (v), la quantité (n) et la température (t) d'un gaz idéal grâce à la constante de Boltzmann (k) :
p * v = n * k * t
Une telle équation n'est pas unidirectionnelle. Si nous avons quatre de ces valeurs, nous pouvons utiliser cette équation pour calculer la cinquième. Pourtant, la traduction de l'équation dans un langage informatique traditionnel nous forcerait à choisir l'une des quantités à calculer en termes de quatre autres. Ainsi, une fonction de calcul de la pression ne peut pas être utilisée pour calculer la température, même si les calculs des deux quantités proviennent de la même équation.
Dans cette section, nous esquissons la conception d'un modèle général des relations linéaires. Nous définissons les contraintes primitives qui s'appliquent à des quantités, par exemple une contrainte adder (a, b, c) qui applique la relation mathématique a + b = c .
Nous définissons aussi un moyen de combiner des contraintes primitives pour exprimer des relations plus complexes. De cette façon, notre programme ressemble à un langage de programmation. Nous combinons des contraintes en construisant un réseau dans lequel les contraintes sont reliées entre elles par des connecteurs. Un connecteur est un objet qui « contient » une valeur et peut participer à une ou plusieurs contraintes.
Par exemple, nous savons que la relation entre les températures mesurées en degrés Fahrenheit et Celsius est :
9 * c = 5 * (f – 32)
Cette équation est une contrainte complexe entre c et f. Une telle contrainte peut être considérée comme un réseau constitué de contraintes primitives de types additionneur, multiplicateur et constante.
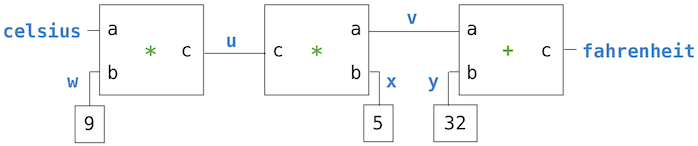
Dans cette figure, on voit sur la gauche une boîte multiplicateur avec trois bornes, étiquetée a, b et c. Celles-ci relient le multiplicateur au reste du réseau de la façon suivante : la borne a est reliée au connecteur celsius, qui contiendra la température en degrés Celsius. La borne b est reliée au connecteur w, qui est lui-même relié à une boîte constante, dont la valeur est 9. La borne c, que la boîte multiplicateur contraint à être le produit d' a et b, est reliée à la borne c d'un autre multiplicateur, dans lequel b est relié à une constante 5 et a relié à l'un des termes d'une contrainte de type additionneur.
Le calcul par un tel réseau se déroule comme suit : lorsqu'un connecteur reçoit une valeur (de la part de l'utilisateur ou par une boîte de contrainte auquel il est relié), il réveille toutes les contraintes auxquelles il est associé (à l' exception de la contrainte qui vient de le réveiller) pour les informer qu'il a une valeur. Chaque boîte de contrainte réveillée sonde alors ses connecteurs pour voir s'il y a suffisamment d'informations pour déterminer une valeur pour un connecteur. Si c'est le cas, la boîte attribue une valeur à ce connecteur, qui réveille alors à son tour toutes les contraintes qui lui sont associées, et ainsi de suite. Par exemple, dans la conversion entre degrés Celsius et Fahrenheit, w, x et y sont alimentées dès le départ par les boîtes constantes à 9, 5, et 32, respectivement. Les connecteurs réveillent les multiplicateurs et l'additionneur, qui déterminent qu'il n'y a pas suffisamment d'informations pour continuer. Si l'utilisateur (ou une autre partie du réseau) attribue une valeur (disons 25) au connecteur celsius, le multiplicateur de gauche est réveillé, et u sera positionné à 25 * 9 = 225. Puis u réveille le second multiplicateur, qui affecte 225/5 = 45 à v, et v réveille l'additionneur, qui fixe le connecteur fahrenheit à 77.
Utilisation du système de contrainte. Pour utiliser le système de contrainte afin d'effectuer le calcul de la température décrit ci-dessus, nous créons d'abord deux connecteurs, nommés celsius et fahrenheit, en appelant le constructeur connector.
>>> celsius = connector('Celsius')
>>> fahrenheit = connector('Fahrenheit')Ensuite, nous relions ces connecteurs à un réseau qui reflète la figure ci-dessus. La fonction converter assemble les différents connecteurs et les contraintes du réseau.
>>> def converter(c, f):
"""Connect c to f with constraints to convert from Celsius to Fahrenheit."""
u, v, w, x, y = [connector() for _ in range(5)]
multiplier(c, w, u)
multiplier(v, x, u)
adder(v, y, f)
constant(w, 9)
constant(x, 5)
constant(y, 32)
>>> converter(celsius, fahrenheit)Nous allons utiliser un système de transmission de messages pour coordonner les contraintes et les connecteurs. Les contraintes sont des dictionnaires qui ne détiennent pas eux-mêmes d'états locaux. Leurs réponses aux messages sont des fonctions non-pures qui changent les connecteurs qu'ils contraignent.
Les connecteurs sont des dictionnaires qui possèdent une valeur courante et répondent aux messages qui manipulent cette valeur. Les contraintes ne changeront pas la valeur des connecteurs directement, mais le feront en envoyant des messages, de sorte que le connecteur peut informer les autres contraintes en réaction au changement. De cette façon, un connecteur représente un nombre, mais encapsule aussi le comportement du connecteur.
Un message que nous pouvons envoyer à un connecteur est une définition de sa valeur. Ici, nous (le 'user') définissons la valeur de celsius à 25.
>>> celsius['set_val']('user', 25)
Celsius = 25
Fahrenheit = 77.0Non seulement la valeur de celsius passe à 25, mais sa valeur se propage à travers le réseau, et la valeur de fahrenheit est également modifiée. Ces changements sont affichés parce que nous avons appelé ces deux connecteurs lorsque nous les construisons.
Maintenant, nous pouvons essayer d'affecter à fahrenheit une nouvelle valeur, disons 212.
>>> fahrenheit['set_val']('user', 212)
Contradiction detected: 77.0 vs 212Le connecteur se plaint qu'il a détecté une contradiction : sa valeur est 77,0, et quelqu'un essaie de le mettre à 212. Si nous voulons vraiment réutiliser le réseau avec de nouvelles valeurs, nous pouvons dire à celsius d'oublier son ancienne valeur :
>>> celsius['forget']('user')
Celsius is forgotten
Fahrenheit is forgottenLe connecteur celsius s'aperçoit que l'utilisateur user, qui avait donné une valeur à l'origine, supprimait maintenant cette valeur ; celsius accepte donc de perdre sa valeur, et il informe le reste du réseau de ce changement. Cette information se propage finalement à Fahrenheit, qui constate maintenant qu'il n'a aucune raison de continuer à croire que sa propre valeur est 77. Par conséquent, il abandonne également sa valeur.
Maintenant que fahrenheit n'a plus de valeur, nous sommes libres de la fixer à 212 :
>>> fahrenheit['set_val']('user', 212)
Fahrenheit = 212
Celsius = 100.0Cette nouvelle valeur se propage à travers le réseau et force celsius à prendre une valeur de 100. Nous avons utilisé le même réseau pour calculer celsius à partir de fahrenheit et pour calculer fahrenheit à partir de celsius. Cette non-directionnalité du calcul est la principale caractéristique des systèmes à base de contraintes.
La mise en œuvre du système de contraintes. Comme nous l'avons vu, les connecteurs sont des dictionnaires qui associent les noms des messages à des fonctions et les valeurs de données. Nous allons mettre en place des connecteurs qui répondent aux messages suivants :
- connector['set_val'](source, value) indique que la source demande au connecteur de positionner sa valeur courante à value.
- connector['has_val']() indique si le connecteur a déjà une valeur.
- connector['val'] renvoie la valeur actuelle du connecteur.
- connector['forget'](source) indique au connecteur que la source lui demande d'oublier sa valeur.
- connector['connect'](source) demande au connecteur de participer à une nouvelle contrainte, la source.
Les contraintes sont aussi des dictionnaires, qui reçoivent des informations des connecteurs au moyen de deux messages :
- constraint['new_val']() indique qu'un connecteur relié à la contrainte a une nouvelle valeur.
- constraint['forget']() indique qu'un connecteur relié à la contrainte a oublié sa valeur.
Lorsque les contraintes reçoivent ces messages, elles les propagent de manière appropriée à d'autres connecteurs.
La fonction adder construit sur trois connecteurs une contrainte d'addition selon laquelle la somme des deux premiers doit être égale au troisième : a + b = c. Pour permettre la propagation de contrainte multidirectionnelle, l'addition doit également préciser qu'il retranche a de c pour obtenir b et soustrait également b de c pour obtenir a.
>>> from operator import add, sub
>>> def adder(a, b, c):
"""The constraint that a + b = c."""
return make_ternary_constraint(a, b, c, add, sub, sub)Nous voudrions mettre en œuvre une contrainte ternaire générique qui utilise les trois connecteurs et trois fonctions de adder pour créer une contrainte qui accepte les messages new_val et forget. Les réponses aux messages sont des fonctions locales qui sont placées dans un dictionnaire appelé contrainte.
>>> def make_ternary_constraint(a, b, c, ab, ca, cb):
"""The constraint that ab(a,b)=c and ca(c,a)=b and cb(c,b) = a."""
def new_value():
av, bv, cv = [connector['has_val']() for connector in (a, b, c)]
if av and bv:
c['set_val'](constraint, ab(a['val'], b['val']))
elif av and cv:
b['set_val'](constraint, ca(c['val'], a['val']))
elif bv and cv:
a['set_val'](constraint, cb(c['val'], b['val']))
def forget_value():
for connector in (a, b, c):
connector['forget'](constraint)
constraint = {'new_val': new_value, 'forget': forget_value}
for connector in (a, b, c):
connector['connect'](constraint)
return constraintLe dictionnaire appelé constraint est une table de distribution, mais représente aussi l'objet contrainte lui-même. Il réagit aux deux messages que les contraintes reçoivent, mais il est également passé comme source de l'argument dans les appels à ses connecteurs.
La fonction locale new_value de la contrainte est appelée chaque fois que la contrainte est informée que l'un de ses connecteurs a une valeur. Cette fonction vérifie d'abord si a et b ont tous deux des valeurs. Si oui, il dit à c de prendre pour valeur la valeur de retour de la fonction ab, qui est add dans le cas d'un additionneur. La contrainte se passe elle-même (constraint) en tant que source de l'argument du connecteur, qui est l'objet additionneur. Si a et b n'ont pas tous les deux une valeur, la contrainte vérifie a et c, et ainsi de suite.
Si la contrainte est informée que l'un de ses connecteurs a oublié sa valeur, il demande à tous ses connecteurs d'oublier désormais leurs valeurs. (Seules les valeurs définies par cette contrainte sont effectivement perdues.)
Un multiplicateur est très similaire à un additionneur.
>>> from operator import mul, truediv
>>> def multiplier(a, b, c):
"""The constraint that a * b = c."""
return make_ternary_constraint(a, b, c, mul, truediv, truediv)Une constante est aussi une contrainte, mais à laquelle on n'envoie jamais de message, car elle ne contient qu'un seul connecteur dont la valeur est fixée lors de la construction.
>>> def constant(connector, value):
"""The constraint that connector = value."""
constraint = {}
connector['set_val'](constraint, value)
return constraintCes trois contraintes sont suffisantes pour mettre en œuvre notre réseau de conversion de température.
Représentation des connecteurs. Un connecteur est représenté comme un dictionnaire qui contient une valeur, mais a également des fonctions de réponse ayant un état local. Le connecteur doit garder la trace de l'informateur (informant) qui lui a donné sa valeur actuelle, et une liste des contraintes auxquelles il participe.
Le constructeur connector a des fonctions locales pour définir et oublier les valeurs qui sont des réactions aux messages reçus des contraintes.
>>> def connector(name=None):
"""A connector between constraints."""
informant = None
constraints = []
def set_value(source, value):
nonlocal informant
val = connector['val']
if val is None:
informant, connector['val'] = source, value
if name is not None:
print(name, '=', value)
inform_all_except(source, 'new_val', constraints)
else:
if val != value:
print('Contradiction detected:', val, 'vs', value)
def forget_value(source):
nonlocal informant
if informant == source:
informant, connector['val'] = None, None
if name is not None:
print(name, 'is forgotten')
inform_all_except(source, 'forget', constraints)
connector = {'val': None,
'set_val': set_value,
'forget': forget_value,
'has_val': lambda: connector['val'] is not None,
'connect': lambda source: constraints.append(source)}
return connectorUn connecteur est à nouveau un dictionnaire faisant office de table de distribution pour les cinq messages utilisés par les contraintes pour communiquer avec les connecteurs. Quatre réponses sont des fonctions, et la dernière est la valeur elle-même.
La fonction locale set_value est appelée quand il y a une demande d'affectation de la valeur du connecteur. Si le connecteur n'a pas de valeur, il prendra la valeur reçue et se souviendra que c'est la contrainte source informant qui lui a demandé de prendre cette valeur. Ensuite, le connecteur informera toutes les contraintes auxquelles il participe, à l'exception de celle qui lui a demandé de prendre cette valeur. On accomplit ceci en utilisant la fonction itérative suivante :
>>> def inform_all_except(source, message, constraints):
"""Inform all constraints of the message, except source."""
for c in constraints:
if c != source:
c[message]()Si l'on demande à un connecteur d'oublier sa valeur, il appelle la fonction locale forget-value, qui vérifie d'abord que la demande provient de la contrainte qui a défini sa valeur à l'origine. Si oui, le connecteur informe les contraintes auxquelles il est associé de la perte de la valeur.
La réponse au message has_val indique si le connecteur a une valeur. La réponse au message connect ajoute la contrainte source à la liste des contraintes.
Le programme de contraintes que nous avons mis en place a introduit de nombreuses idées qui apparaîtront à nouveau dans la programmation orientée objet. Les contraintes et les connecteurs sont les deux abstractions qui sont manipulées par le biais de messages. Lorsque la valeur d'un connecteur est modifiée, ce changement est effectué par un message qui non seulement modifie la valeur, mais effectue la validation (vérification de la source) et propage ses effets (informer les autres contraintes). En fait, nous allons utiliser une architecture similaire de dictionnaires avec des clés sous forme de chaîne et des valeurs fonctionnelles pour mettre en œuvre un système orienté objet plus loin dans ce tutoriel.
5. Programmation orientée objet ▲
La programmation orientée objet (POO) est une méthode d'organisation de programmes qui rassemble bon nombre des idées présentées dans ce tutoriel. Comme les fonctions d'abstraction des données, les classes créent des barrières d'abstraction entre l'utilisation et la mise en œuvre des données. Comme les dictionnaires ou tables de distribution, les objets répondent à des demandes comportementales. Comme les structures de données mutables, les objets ont un état local qui n'est pas directement accessible depuis l'environnement global. Le système d'objets de Python fournit une syntaxe pratique pour promouvoir l'utilisation de ces techniques pour l'organisation de programmes. Une grande partie de cette syntaxe est commune à d'autres langages de programmation orientés objet.
Le système d'objet offre plus que de la commodité. Il permet une nouvelle métaphore pour concevoir des programmes dans lesquels plusieurs agents indépendants interagissent au sein de l'ordinateur. Chaque objet regroupe un état local et un comportement d'une manière qui résume la complexité des deux. Les objets communiquent entre eux et les résultats utiles sont calculés à la suite de leur interaction. Non seulement les objets transmettent-ils des messages, mais ils partagent également un comportement avec d'autres objets du même type et héritent des caractéristiques des types apparentés.
Le paradigme de la programmation orientée objet a son propre vocabulaire qui prend en charge la métaphore de l'objet. Nous avons vu qu'un objet est une donnée qui a des méthodes et des attributs, accessibles par notation pointée. Chaque objet a également un type, appelé sa classe. Pour créer de nouveaux types de données, nous implémentons de nouvelles classes.
5-1. Objets et classes ▲
Une classe sert de modèle pour tous les objets dont le type est cette classe. Chaque objet est une instance d'une classe particulière. Les objets que nous avons utilisés jusqu'ici ont tous des classes intégrées au langage, mais il est également possible de créer de nouvelles classes définies par l'utilisateur. Une définition de classe spécifie les attributs et les méthodes partagés entre les objets de cette classe. Nous présenterons la définition d'une classe en revisitant l'exemple d'un compte bancaire.
Lors de l'introduction de l'état local, nous avons vu que les comptes bancaires sont naturellement modélisés comme des valeurs mutables qui ont un solde (balance). Un objet compte bancaire doit avoir une méthode de retrait (withdraw) qui met à jour le solde du compte et renvoie le montant demandé, s'il est disponible. Pour compléter l'abstraction : un compte bancaire doit être en mesure de renvoyer son solde (balance) courant et le nom du titulaire (holder) du compte, et permettre le dépôt (deposit) d'un montant.
Une classe Account nous permet de créer plusieurs instances de comptes bancaires. L'acte de créer une nouvelle instance d'objet s'appelle une instanciation de la classe. La syntaxe en Python pour instancier une classe est identique à la syntaxe d'appel d'une fonction. Dans ce cas, nous appelons Account avec l'argument 'Kirk', le nom du titulaire du compte.
>>> a = Account('Kirk')Un attribut d'un objet est une paire nom-valeur associée à l'objet, accessible par notation pointée. Les attributs spécifiques à un objet particulier, par opposition aux attributs communs à tous les objets d'une classe, sont appelés attributs d'instance. Chaque compte a son propre solde et son propre nom de compte ; ce sont des exemples d'attributs d'instance. Dans la communauté de programmation plus large, les attributs d'instance peuvent également s'appeler champs, propriétés ou variables d'instance.
>>> a.holder
'Kirk'
>>> a.balance
0Les fonctions qui s'appliquent à un objet ou effectuent des calculs spécifiques à un objet s'appellent des méthodes. Les valeurs de retour d'une méthode peuvent dépendre des attributs de l'objet ; une méthode peut aussi avoir pour effet de modifier un ou plusieurs attributs d'un objet. Par exemple, deposit est une méthode de notre objet Account a. Elle prend un argument, le montant à déposer, modifie l'attribut solde (balance) de l'objet et renvoie le solde résultant.
>>> a.deposit(15)
15Nous disons que les méthodes sont invoquées sur un objet particulier. Suite à l'invocation de la méthode withdraw, soit le retrait est approuvé et le montant est déduit du solde, soit la demande est refusée et la méthode renvoie un message d'erreur.
>>> a.withdraw(10) # The withdraw method returns the balance after withdrawal
5
>>> a.balance # The balance attribute has changed
5
>>> a.withdraw(10)
'Insufficient funds'Comme on le voit ci-dessus, le comportement d'une méthode peut dépendre des attributs changeants de l'objet. Deux appels successifs à withdraw avec le même argument renvoient des résultats différents.
5-2. Définition de classes ▲
Les classes définies par l'utilisateur sont créées par des déclarations class, constituées d'une seule clause. Une déclaration de classe définit le nom de la classe, puis inclut une suite d'instructions pour définir les attributs de la classe :
class <name>:
<suite>Lorsqu'une déclaration de classe est exécutée, une nouvelle classe est créée et liée à <name> dans le premier cadre de l'environnement courant. La suite est ensuite exécutée. Tout nom lié dans la <suite> d'une déclaration class, via des instructions def ou des affectations, crée ou modifie des attributs de la classe.
Les classes sont généralement organisées autour de la manipulation des attributs d'instance, qui sont les paires nom-valeur associées à chaque instance de cette classe. La classe spécifie les attributs d'instance de ses objets en définissant une méthode d'initialisation de nouveaux objets. Par exemple, une partie de l'initialisation d'un objet de la classe Account consiste à lui affecter un solde de départ de 0.
La <suite> d'une déclaration de class contient des instructions def qui définissent de nouvelles méthodes pour les objets de cette classe. La méthode qui initialise les objets a un nom spécial dans Python, __init__ (deux caractères de soulignement de chaque côté du mot « init »), et s'appelle le constructeur de la classe.
>>> class Account:
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holderLa méthode __init__ de la classe Account a deux paramètres formels. Le premier, self, est lié à l'objet Account nouvellement créé. Le second paramètre, account_holder (titulaire du compte), est lié à l'argument passé à la classe lorsqu'elle est appelée à être instanciée.
Le constructeur lie l'attribut d'instance balance à 0. Il lie également le nom d'attribut holder à la valeur du nom account_holder. Le paramètre formel account_holder est un nom local dans la méthode __init__. En revanche, le nom holder lié via l'instruction d'affectation finale est persistant, car il est stocké en tant qu'attribut de self, via la notation pointée.
Après avoir défini la classe Account, nous pouvons l'instancier :
>>> a = Account('Kirk')Cet « appel » à la classe Account crée un nouvel objet qui est une instance d'Account, puis appelle la fonction constructeur __init__ avec deux arguments : l'objet nouvellement créé et la chaîne de caractères 'Kirk'. Par convention, nous utilisons le nom de paramètre self pour le premier argument d'un constructeur, car il est lié à l'objet instancié. Cette convention est adoptée dans pratiquement tous les programmes Python.
Maintenant, nous pouvons accéder au solde et au titulaire de l'objet a en utilisant la notation pointée :
>>> a.balance
0
>>> a.holder
'Kirk'Identité. Chaque nouvelle instance de compte a son propre attribut de solde, dont la valeur est indépendante des autres objets de la même classe.
>>> b = Account('Spock')
>>> b.balance = 200
>>> [acc.balance for acc in (a, b)]
[0, 200]Pour instaurer cette séparation, chaque objet instance d'une classe définie par l'utilisateur a une identité unique. L'identité de l'objet est comparée en utilisant les opérateurs is et not :
>>> a is a
True
>>> a is not b
TrueBien qu'ils soient construits à partir d'appels identiques, les objets liés à a et b ne sont pas identiques. Comme d'habitude, lier un objet à un nouveau nom en utilisant l'assignation ne crée pas un nouvel objet.
>>> c = a
>>> c is a
TrueLes nouveaux objets dont les classes sont définies par l'utilisateur sont créés uniquement lorsqu'une classe (comme Account) est instanciée avec une syntaxe d'appel d'expression.
Méthodes. Les méthodes sont définies (comme les fonctions) par une instruction def dans la suite d'une déclaration de type class. Ci-dessous, deposit et withdraw sont définies comme des méthodes sur les objets de la classe Account.
>>> class Account:
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
def deposit(self, amount):
self.balance = self.balance + amount
return self.balance
def withdraw(self, amount):
if amount > self.balance:
return 'Insufficient funds'
self.balance = self.balance - amount
return self.balanceBien que les définitions de méthodes ne diffèrent pas des définitions de fonctions dans la façon dont elles sont déclarées, les définitions de méthodes ont un effet différent lorsqu'elles sont exécutées. La valeur de fonction créée par une instruction def dans une déclaration class est liée au nom déclaré, mais liée localement dans la classe en tant qu'attribut. Cette valeur est invoquée comme une méthode utilisant la notation pointée depuis une instance de la classe.
Comme nous l'avons déjà vu, chaque définition de méthode inclut un premier paramètre spécial self, qui est lié à l'objet sur lequel la méthode est invoquée. Par exemple, supposons que la méthode deposit soit invoquée sur un objet particulier de la classe Account et qu'elle ne passe qu'un seul argument : le montant déposé. L'objet lui-même est lié à self, tandis que l'argument est lié à amount (le montant du dépôt). Toutes les méthodes invoquées ont accès à l'objet via le paramètre self, et peuvent ainsi toutes accéder et manipuler l'état de l'objet.
Pour invoquer ces méthodes, nous utilisons de nouveau la notation pointée, comme on le voit ci-dessous :
>>> spock_account = Account('Spock')
>>> spock_account.deposit(100)
100
>>> spock_account.withdraw(90)
10
>>> spock_account.withdraw(90)
'Insufficient funds'
>>> spock_account.holder
'Spock'Lorsqu'une méthode est invoquée via la notation pointée, l'objet lui-même (lié à spock_account, dans ce cas) joue un double rôle. D'abord, il détermine ce que le nom withdraw signifie ; withdraw n'est pas un nom dans l'environnement, mais un nom qui est local dans la classe Account. Deuxièmement, il est lié au premier paramètre self lorsque la méthode de withdraw est invoquée.
5-3. Passage de message et expressions pointées ▲
Les méthodes, qui sont définies dans les classes, et les attributs d'instance, qui sont généralement alimentés dans les constructeurs, sont les éléments fondamentaux de la programmation orientée objet. Ces deux concepts répliquent une grande partie du comportement d'un dictionnaire de distribution dans un message transmettant l'implémentation d'une valeur de données. Les objets prennent des messages en utilisant la notation pointée, mais au lieu que ces messages soient des clefs d'un dictionnaire, ils sont des noms locaux à une classe. Les objets ont également des valeurs d'état local nommées (les attributs d'instance), mais cet état peut être accédé et manipulé en utilisant la notation pointée, sans avoir à employer d'instructions nonlocal dans l'implémentation.
L'idée centrale dans le passage des messages était que les valeurs de données devaient avoir un comportement en répondant aux messages qui sont pertinents pour le type abstrait qu'ils représentent. La notation pointée est une caractéristique syntaxique de Python qui formalise la métaphore du passage du message. L'avantage d'utiliser un langage avec un système objet intégré est que le passage de message peut interagir de manière transparente avec d'autres fonctionnalités de langage, telles que des instructions d'affectation. Nous n'avons pas besoin de messages différents pour nos « accesseurs » et nos « mutateurs » permettant d'interagir avec la valeur associée à un nom d'attribut local ; la syntaxe du langage nous permet d'utiliser directement le nom du message.
Expressions pointées. Le fragment de code spock_account.deposit s'appelle une expression pointée. Une expression pointée consiste en une expression, un point et un nom :
<expression> . <name>L'<expression> peut être une expression Python valide quelconque, mais <name> doit être un nom simple (pas une expression qui s'évalue à un nom). Une expression pointée s'évalue à la valeur de l'attribut ayant le nom (<name>) donné, pour l'objet qui est la valeur de l'<expression>.
La fonction intégrée au langage getattr renvoie également un attribut pour un objet par son nom. C'est une fonction équivalente à la notation pointée. En utilisant getattr, nous pouvons rechercher un attribut en utilisant une chaîne, comme nous l'avons fait avec un dictionnaire de distribution.
>>> getattr(spock_account, 'balance')
10Nous pouvons également tester si un objet a un attribut nommé avec hasattr :
>>> hasattr(spock_account, 'deposit')
TrueLes attributs d'un objet incluent tous ses attributs d'instance, ainsi que tous les attributs (y compris les méthodes) définis dans sa classe. Les méthodes sont des attributs de la classe qui nécessitent un traitement spécial.
Méthodes et fonctions. Lorsqu'une méthode est appelée sur un objet, cet objet est implicitement transmis en tant que premier argument de la méthode. C'est-à-dire que l'objet qui représente la valeur d'<expression> à la gauche du point est passé automatiquement en tant que premier argument de la méthode nommée du côté droit de l'expression pointée. Il en résulte que l'objet est lié au paramètre self.
Pour réaliser cette liaison automatique avec self, Python distingue les fonctions, que nous avons créées depuis le début de ce livre, et les méthodes liées, qui associent une fonction et l'objet sur lequel cette méthode sera appelée. Une valeur de méthode liée est déjà associée à son premier argument, l'instance sur laquelle elle a été invoquée, qui sera appelée self lors de l'appel de la méthode.
Nous pouvons voir la différence dans l'interpréteur interactif en appelant type sur les valeurs renvoyées par des expressions pointées. En tant qu'attribut d'une classe, une méthode est juste une fonction, mais en tant qu'attribut d'une instance, c'est une méthode liée :
>>> type(Account.deposit)
<class 'function'>
>>> type(spock_account.deposit)
<class 'method'>Ces deux résultats ne diffèrent que par le fait que le premier est une fonction standard à deux arguments avec des paramètres self et amount. La seconde est une méthode à un argument, où le nom self sera automatiquement lié à l'objet spock_account lorsque la méthode sera appelée, tandis que le paramètre sera lié à l'argument passé à la méthode. Ces deux valeurs, qu'il s'agisse de valeurs de fonction ou de valeurs de méthode liées, sont associées au même corps de la fonction deposit.
Nous pouvons appeler deposit de deux façons : en tant que fonction et en tant que méthode liée. Dans le premier cas, nous devons explicitement fournir un argument pour le paramètre self. Dans le second cas, le paramètre self est automatiquement lié.
>>> Account.deposit(tom_account, 1001) # The deposit function requires 2 arguments
1011
>>> tom_account.deposit(1000) # The deposit method takes 1 argument
2011La fonction getattr se comporte exactement comme la notation pointée : si son premier argument est un objet mais que le nom est une méthode définie dans la classe, alors getattr renvoie une valeur de méthode liée. D'un autre côté, si le premier argument est une classe, alors getattr renvoie directement la valeur de l'attribut, qui est une fonction simple.
Guide pratique : conventions de nommage. Les noms de classes sont classiquement écrits en utilisant la convention CapWords (également appelée CamelCase parce que les majuscules au milieu d'un nom suggèrent les bosses d'un chameau). Les noms de méthode suivent la convention standard de nommage des fonctions et utilisent des mots en minuscules séparés par des caractères de soulignement.
Dans certains cas, il existe des variables et des méthodes d'instance liées à la maintenance et à la cohérence d'un objet que nous ne voulons pas que les utilisateurs de l'objet voient ou utilisent. Elles ne font pas partie de l'abstraction définie par une classe, mais font plutôt partie de l'implémentation. La convention de Python stipule que si un nom d'attribut commence par un trait de soulignement, il ne doit être employé que dans les méthodes de la classe elle-même, mais non par les utilisateurs de la classe.
5-4. Attributs de classe ▲
Certains attributs sont partagés entre tous les objets d'une classe donnée. Ces attributs sont associés à la classe elle-même, plutôt qu'à une quelconque instance individuelle de la classe. Par exemple, supposons qu'une banque paie des intérêts sur le solde des comptes à un taux d'intérêt fixe. Ce taux d'intérêt peut changer, mais il s'agit d'une valeur unique partagée pour tous les comptes.
Les attributs de classe sont créés par des instructions d'affectation dans la suite d'une déclaration de class, en dehors de toute définition de méthode. Dans la communauté de développeurs plus large, les attributs de classe peuvent aussi s'appeler variables de classe ou variables statiques. La déclaration de classe suivante crée un attribut de classe nommé interest pour la classe Account :
>>> class Account(object):
interest = 0.02 # A class attribute
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
# Additional methods would be defined hereCet attribut est toujours accessible depuis n'importe quelle instance de la classe.
>>> tom_account = Account('Tom')
>>> jim_account = Account('Jim')
>>> tom_account.interest
0.02
>>> jim_account.interest
0.02Toutefois, une instruction d'affectation sur un attribut de classe modifie la valeur de l'attribut pour toutes les instances de la classe.
>>> Account.interest = 0.04
>>> tom_account.interest
0.04
>>> jim_account.interest
0.04Noms d'attribut. Nous avons introduit suffisamment de complexité dans notre système d'objets pour que nous devions spécifier comment les noms se résolvent en des attributs particuliers. Après tout, nous pourrions facilement avoir un attribut de classe et un attribut d'instance ayant le même nom.
Comme nous l'avons vu, une expression pointée consiste en une expression, un point et un nom :
<expression> . <name>Pour évaluer une expression pointée :
- Évaluez l'<expression> à gauche du point, ce qui donne l'objet de l'expression pointée.
- <name> est comparé aux attributs d'instance de cet objet ; si un attribut d'instance portant ce nom existe, sa valeur est renvoyée.
- Si <name> n'apparaît pas parmi les attributs d'instance, alors <name> est recherché dans la classe, ce qui donne une valeur d'attribut de classe.
- Cette valeur est renvoyée sauf s'il s'agit d'une fonction, auquel cas une méthode liée est renvoyée à la place.
Dans cette procédure d'évaluation, les attributs d'instance sont détectés avant les attributs de classe, de même que les noms locaux ont priorité sur les noms globaux dans un environnement. Les méthodes définies dans la classe sont combinées avec l'objet de l'expression pointée pour former une méthode liée pendant la quatrième étape de cette procédure d'évaluation. La procédure de recherche d'un nom dans une classe a des nuances supplémentaires qui apparaîtront sous peu, quand nous aurons introduit la notion d'héritage de classe.
Affectation d'attribut. Toutes les instructions d'affectation qui contiennent une expression pointée du côté gauche de l'affectation modifient les attributs de l'objet de cette expression pointée. Si l'objet est une instance, l'affectation définit un attribut d'instance. Si l'objet est une classe, alors l'affectation définit un attribut de classe. En conséquence de cette règle, l'affectation à un attribut d'un objet ne peut pas affecter les attributs de sa classe. Les exemples ci-dessous illustrent cette distinction.
Si nous affectons à l'attribut d'intérêt d'une instance de compte, nous créons un nouvel attribut d'instance qui a le même nom que l'attribut de classe existant.
>>> jim_account.interest = 0.08et cette valeur d'attribut sera renvoyée par une expression pointée :
>>> jim_account.interest
0.08Toutefois, l'attribut de classe interest conserve sa valeur d'origine, qui est renvoyée pour tous les autres comptes :
>>> tom_account.interest
0.04Les modifications apportées à l'attribut de classe affecteront tom_account, mais l'attribut d'instance de jim_account ne sera pas affecté.
>>> Account.interest = 0.05 # changing the class attribute
>>> tom_account.interest # changes instances without like-named instance attributes
0.05
>>> jim_account.interest # but the existing instance attribute is unaffected
0.085-5. Héritage ▲
Lorsque nous travaillons dans le paradigme de la programmation orientée objet, nous constatons souvent que différents types de données abstraites sont liés. En particulier, nous trouvons que les classes similaires diffèrent dans leur degré de spécialisation. Deux classes peuvent avoir des attributs similaires, mais l'une représente un cas particulier de l'autre.
Par exemple, nous souhaitons implémenter un compte-chèques (CheckingAccount), différent d'un compte standard. Un compte-chèques facture une commission égale à 1 $ pour chaque retrait et offre un taux d'intérêt plus bas. Voici le comportement souhaité :
>>> ch = CheckingAccount('Tom')
>>> ch.interest # Lower interest rate for checking accounts
0.01
>>> ch.deposit(20) # Deposits are the same
20
>>> ch.withdraw(5) # withdrawals decrease balance by an extra charge
14Un CheckingAccount est une spécialisation d'un Account. Dans la terminologie OOP, le compte générique servira de classe de base de CheckingAccount, alors que CheckingAccount sera une sous-classe de Account. (Les termes classe parente, classe mère et superclasse sont également utilisés pour la classe de base, tandis que les termes classe enfant ou classe fille sont également employés pour la sous-classe.)
Une sous-classe hérite des attributs de sa classe de base, mais peut remplacer certains attributs, y compris certaines méthodes. Avec l'héritage, nous spécifions seulement ce qui est différent entre la sous-classe et la classe de base. Tout ce que nous laissons non spécifié dans la sous-classe est automatiquement supposé se comporter exactement comme la classe de base.
L'héritage a aussi un rôle dans notre métaphore de l'objet, en plus d'être une caractéristique organisationnelle utile. L'héritage est censé représenter des relations de type est-un ou est-une (is-a) entre les classes, par opposition aux relations a-un (has-a). Un compte-chèques est-un type de compte spécifique. Avoir un CheckingAccount qui hérite de Account est donc une utilisation appropriée de l'héritage. D'un autre côté, une banque a une liste de comptes bancaires qu'elle gère, donc la liste de compte ne doit pas hériter de la banque (ni l'inverse). Au lieu de cela, une liste d'objets de compte s'exprimerait naturellement sous la forme d'attribut d'instance d'un objet banque.
5-6. Utilisation de l'héritage ▲
Nous spécifions l'héritage en plaçant la classe parente entre parenthèses dans la déclaration de la classe fille.
Pour commencer, nous donnons une implémentation complète de la classe Account, qui inclut les docstrings pour la classe et ses méthodes.
>>> class Account(object):
"""Un compte bancaire qui a un solde non négatif."""
interest = 0.02
def __init__(self, account_holder):
self.balance = 0
self.holder = account_holder
def deposit(self, amount):
"""Augmenter le solde du compte et retourner le nouveau solde."""
self.balance = self.balance + amount
return self.balance
def withdraw(self, amount):
"""Diminuer le solde du compte et retourner le nouveau solde."""
if amount > self.balance:
return 'Insufficient funds'
self.balance = self.balance - amount
return self.balanceUne implémentation complète de CheckingAccount figure ci-dessous.
>>> class CheckingAccount(Account):
"""Un compte bancaire qui facture les retraits."""
withdraw_charge = 1
interest = 0.01
def withdraw(self, amount):
return Account.withdraw(self, amount + self.withdraw_charge)Ici, nous introduisons un attribut de classe withdraw_charge spécifique à la classe CheckingAccount. Nous affectons une valeur inférieure à l'attribut interest. Nous définissons également une nouvelle méthode de retrait withdraw pour remplacer le comportement défini dans la classe Account. En l'absence d'autres instructions dans la suite de classes, tous les autres comportements sont hérités de la classe de base Account.
>>> checking = CheckingAccount('Sam')
>>> checking.deposit(10)
10
>>> checking.withdraw(5)
4
>>> checking.interest
0.01L'expression checking.deposit évalue une méthode liée à la création de dépôts, qui a été définie dans la classe Account. Lorsque Python résout un nom dans une expression pointée qui n'est pas un attribut de l'instance, il recherche le nom dans la classe. En fait, le fait de « rechercher » un nom dans une classe essaie de trouver ce nom dans chaque classe parente de la chaîne d'héritage de la classe de l'objet d'origine. Nous pouvons définir cette procédure de manière récursive. Pour rechercher un nom dans une classe :
- S'il correspond à un attribut dans la classe, renvoyez la valeur de l'attribut.
- Sinon, recherchez le nom dans la classe parente, s'il y en a une.
Dans le cas de deposit, Python aurait recherché le nom en premier sur l'instance, puis dans la classe CheckingAccount. Enfin, il apparaîtrait dans la classe Account, où deposit est défini. Selon notre règle d'évaluation pour les expressions pointées, puisque deposit est une fonction recherchée dans la classe pour l'instance checking, l'expression pointée est évaluée en une valeur de méthode liée. Cette méthode est invoquée avec l'argument 10, qui appelle la méthode de dépôt avec self lié à l'objet de checking et le montant amount lié à 10.
La classe d'un objet reste constante tout au long de ce processus. Même si la méthode deposit a été trouvée dans la classe Account, deposit est appelée avec self lié à une instance de CheckingAccount, et non d'Account.
Appel des ancêtres. Les attributs qui ont été remplacés sont toujours accessibles via les objets de classe. Par exemple, nous avons implémenté la méthode de retrait de CheckingAccount en appelant la méthode withdraw de Account avec un argument qui incluait la withdraw_charge.
Notez que nous avons appelé self.withdraw_charge plutôt que CheckingAccount.withdraw_charge qui serait équivalent. L'avantage de la première solution par rapport à la seconde est qu'une classe qui hérite de CheckingAccount peut modifier la commission (withdraw_charge). Si tel est le cas, nous aimerions que notre nouvelle classe trouve cette nouvelle valeur plutôt que l'ancienne.
5-7. Héritage multiple ▲
Python prend en charge le concept d'une sous-classe héritant des attributs de plusieurs classes de base, une fonctionnalité de langage appelée héritage multiple.
Supposons que nous ayons un compte d'épargne (SavingsAccount) qui hérite d'Account, mais facture des frais minimes aux clients chaque fois qu'ils effectuent un dépôt.
>>> class SavingsAccount(Account):
deposit_charge = 2
def deposit(self, amount):
return Account.deposit(self, amount - self.deposit_charge)Ensuite, un as du marketing imagine un compte « vu à la télé », AsSeenOnTVAccount, combinant les meilleures caractéristiques de CheckingAccount et de SavingsAccount : frais de retrait, frais de dépôt et un taux d'intérêt bas. C'est à la fois un compte-chèques et un compte d'épargne, tout-en-un ! « Si nous le faisons », affirme notre gourou, « quelqu'un va s'inscrire et payer tous ces frais, nous allons même leur donner un dollar. »
>>> class AsSeenOnTVAccount(CheckingAccount, SavingsAccount):
def __init__(self, account_holder):
self.holder = account_holder
self.balance = 1 # A free dollar!En fait, cette implémentation est complète. Les retraits et les dépôts génèrent des frais, en utilisant respectivement les définitions de fonction dans CheckingAccount et SavingsAccount.
>>> such_a_deal = AsSeenOnTVAccount("John")
>>> such_a_deal.balance
1
>>> such_a_deal.deposit(20) # $2 fee from SavingsAccount.deposit
19
>>> such_a_deal.withdraw(5) # $1 fee from CheckingAccount.withdraw
13Les références non ambiguës sont résolues correctement comme prévu :
>>> such_a_deal.deposit_charge
2
>>> such_a_deal.withdraw_charge
1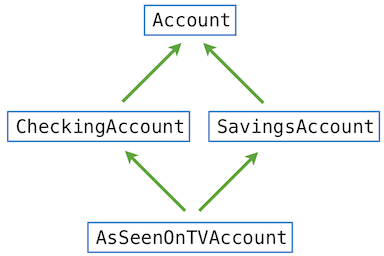
Mais qu'en est-il lorsque la référence est ambiguë, comme la référence à la méthode withdraw définie dans Account et dans CheckingAccount ? La figure ci-dessous illustre un graphe d'héritage pour la classe AsSeenOnTVAccount. Chaque flèche pointe d'une sous-classe vers une classe de base.
Pour une forme « en diamant » simple comme celle-ci, Python résout les noms de gauche à droite, puis vers le haut. Dans cet exemple, Python recherche un nom d'attribut dans les classes suivantes, dans l'ordre, jusqu'à ce qu'un attribut portant ce nom soit trouvé :
AsSeenOnTVAccount, CheckingAccount, SavingsAccount, Account, objectIl n'y a pas de solution correcte au problème de l'ordre des héritages, car il y a des cas dans lesquels nous préférons donner la priorité à certaines classes héritées plutôt qu'à d'autres. Cependant, tout langage de programmation prenant en charge l'héritage multiple doit sélectionner un ordre d'une manière cohérente, afin que les utilisateurs du langage puissent prédire le comportement de leurs programmes.
Lectures complémentaires. Python résout ce nom en utilisant un algorithme récursif appelé C3 Method Resolution Ordering. L'ordre de résolution de méthode de n'importe quelle classe peut être interrogé en utilisant la méthode mro sur toutes les classes.
>>> [c.__name__ for c in AsSeenOnTVAccount.mro()]
['AsSeenOnTVAccount', 'CheckingAccount', 'SavingsAccount', 'Account', 'object']L'algorithme précis pour trouver l'ordre de résolution de méthode dépasse le cadre du présent texte, mais est décrit par l'auteur principal de Python avec une référence à l'article original.
5-8. Le rôle des objets ▲
Le système objet Python est conçu pour rendre l'abstraction des données et le passage des messages à la fois pratique et flexible. La syntaxe spécialisée des classes, des méthodes, de l'héritage et des expressions pointées nous permet de formaliser la métaphore de l'objet dans nos programmes, ce qui améliore notre capacité à organiser de grands programmes.
En particulier, nous aimerions que notre système d'objets favorise une séparation des préoccupations entre les différents aspects du programme. Chaque objet dans un programme encapsule et gère une partie de l'état du programme, et chaque déclaration de classe définit les fonctions qui implémentent une partie de la logique globale du programme. Les barrières d'abstraction imposent des frontières entre les différents aspects d'un grand programme.
La programmation orientée objet est particulièrement bien adaptée aux programmes qui modélisent des systèmes ayant des parties séparées mais en interaction. Par exemple, différents utilisateurs interagissent dans un réseau social, différents personnages interagissent dans un jeu et différentes formes interagissent dans une simulation physique. Quand ils représentent ce genre de systèmes, les objets d'un programme modélisent souvent naturellement les objets du système modélisé, et les classes représentent leurs types et leurs relations.
D'un autre côté, il se peut que les classes ne fournissent pas le meilleur mécanisme pour mettre en œuvre certaines abstractions. Les abstractions fonctionnelles fournissent une métaphore plus naturelle pour représenter les relations entre les entrées et les sorties. Il ne faut pas se sentir obligé d'adapter chaque élément de la logique d'un programme à une classe, en particulier quand la définition des fonctions indépendantes pour manipuler des données est plus naturelle. Les fonctions peuvent également appliquer une séparation des préoccupations.
Les langages multiparadigmes comme Python permettent aux programmeurs d'adapter les paradigmes organisationnels aux problèmes appropriés. Apprendre à identifier quand introduire une nouvelle classe, ou au contraire une nouvelle fonction, afin de simplifier ou modulariser un programme, est une compétence importante de conception en génie logiciel.
6. Implémentation de classes et d'objets ▲
Lorsque nous travaillons dans le paradigme de la programmation orientée objet, nous utilisons la métaphore de l'objet pour guider l'organisation de nos programmes. L'essentiel de la façon de représenter et de manipuler les données s'exprime dans les déclarations de classe. Dans cette section, nous voyons que les classes et les objets peuvent eux-mêmes être représentés en utilisant seulement des fonctions et des dictionnaires. Le but de la mise en œuvre d'un système objet de cette manière est d'illustrer que l'utilisation de la métaphore de l'objet ne nécessite pas de langage de programmation spécial. Les programmes peuvent être orientés objet, même dans les langages de programmation qui n'ont pas de système objet intégré.
Pour implémenter des objets, nous abandonnerons la notation pointée (qui nécessite un support de langue intégré), mais créerons des dictionnaires de répartition qui se comporteront de la même manière que les éléments du système objet intégré. Nous avons déjà vu comment implémenter un comportement de passage de message à travers des dictionnaires de distribution. Pour implémenter un système objet dans son intégralité, nous envoyons des messages entre instances, classes et classes parentes, qui sont tous des dictionnaires contenant des attributs.
Nous n'implémenterons pas tout le système d'objets de Python, qui inclut des fonctionnalités que nous n'avons pas couvertes dans ce texte (par exemple, les métaclasses et les méthodes statiques). Nous nous concentrerons plutôt sur des classes définies par l'utilisateur sans héritage multiple et sans comportement introspectif (comme retourner la classe d'une instance). Notre implémentation n'est pas destinée à suivre la spécification précise du système de types de Python. Au lieu de cela, il est conçu pour implémenter la fonctionnalité de base qui permet la métaphore de l'objet.
6-1. Instances ▲
Nous commençons avec des instances. Une instance a des attributs nommés, tels que le solde d'un compte, qui peuvent être définis et récupérés. Nous implémentons une instance utilisant un dictionnaire de distribution qui répond aux messages de types « accesseur » et « mutateur » sur les valeurs d'attribut. Les attributs eux-mêmes sont stockés dans un dictionnaire local appelé attributes.
Comme nous l'avons vu précédemment dans ce tutoriel, les dictionnaires eux-mêmes sont des types de données abstraits. Nous avons implémenté des dictionnaires avec des listes, nous avons implémenté des listes avec des paires, et nous avons implémenté des paires avec des fonctions. Comme nous implémentons un système d'objets en termes de dictionnaires, gardez à l'esprit que nous pourrions tout aussi bien implémenter des objets en n'utilisant que des fonctions.
Pour commencer notre implémentation, nous supposons que nous avons une implémentation de classe qui peut rechercher les noms qui ne font pas partie de l'instance. Nous passons à make_instance une classe sous la forme du paramètre cls :
>>> def make_instance(cls):
"""Return a new object instance, which is a dispatch dictionary."""
def get_value(name):
if name in attributes:
return attributes[name]
else:
value = cls['get'](name)
return bind_method(value, instance)
def set_value(name, value):
attributes[name] = value
attributes = {}
instance = {'get': get_value, 'set': set_value}
return instanceinstance est un dictionnaire de distribution qui répond aux messages get et set. Le message set correspond à l'affectation d'attribut dans le système objet de Python : tous les attributs assignés sont stockés directement dans le dictionnaire d'attributs local de l'objet. Dans get, si le nom name n'apparaît pas dans le dictionnaire des attributs locaux attributes, alors il est recherché dans la classe. Si la value retournée par cls est une fonction, elle doit être liée à l'instance.
Valeurs de méthode liées. La fonction get_value dans make_instance trouve un attribut nommé dans sa classe avec get, puis appelle bind_method. La liaison d'une méthode s'applique uniquement aux valeurs de fonction et crée une valeur de méthode liée à partir d'une valeur de fonction en insérant l'occurrence en tant que premier argument :
>>> def bind_method(value, instance):
"""Return a bound method if value is callable, or value otherwise."""
if callable(value):
def method(*args):
return value(instance, *args)
return method
else:
return valueQuand une méthode est appelée, le premier paramètre self sera lié à la valeur de instance par cette définition.
6-2. Classes ▲
Une classe est aussi un objet, à la fois dans le système objet de Python et dans le système que nous mettons en place ici. Pour simplifier, nous disons que les classes n'ont pas elles-mêmes de classes. (En Python, les classes ont des classes, presque toutes les classes partagent la même classe, appelée type.) Une classe peut répondre à des messages get et set, ainsi qu'au message new :
>>> def make_class(attributes, base_class=None):
"""Return a new class, which is a dispatch dictionary."""
def get_value(name):
if name in attributes:
return attributes[name]
elif base_class is not None:
return base_class['get'](name)
def set_value(name, value):
attributes[name] = value
def new(*args):
return init_instance(cls, *args)
cls = {'get': get_value, 'set': set_value, 'new': new}
return clsContrairement à une instance, la fonction get pour les classes n'interroge pas sa classe lorsqu'un attribut est introuvable, mais interroge à la place sa classe parente base_class. Aucune méthode de liaison n'est requise pour les classes.
Initialisation. La fonction new dans make_class appelle init_instance, qui commence par créer une nouvelle instance, puis appelle une méthode appelée __init__.
>>> def init_instance(cls, *args):
"""Return a new object with type cls, initialized with args."""
instance = make_instance(cls)
init = cls['get']('__init__')
if init:
init(instance, *args)
return instanceCette dernière fonction complète notre système objet. Nous avons maintenant des instances, qui sont mutées (set) localement, mais retombent dans leurs classes sur un accès en lecture (get). Après avoir recherché un nom dans sa classe, une instance se lie aux valeurs de fonction pour créer des méthodes. Enfin, les classes peuvent construire de nouvelles (new) instances, et elles appliquent leur constructeur __init__ immédiatement après la création de l'instance.
Dans ce système d'objet, la seule fonction qui doive être appelée par l'utilisateur est create_class. Toutes les autres fonctionnalités sont activées par le passage de message. De même, le système objet de Python est appelé via l'instruction de class, et toutes ses autres fonctionnalités sont activées via des expressions pointées et des appels aux classes.
6-3. Utiliser des objets implémentés ▲
Revenons maintenant à l'exemple de compte bancaire de la section précédente. En utilisant le système d'objets que nous venons de mettre en place, nous allons créer une classe Account, une classe fille CheckingAccount et une instance de chacune de ces classes.
La classe Account est créée à l'aide d'une fonction create_account_class, dont la structure est similaire à une instruction de class dans Python, mais se termine par un appel à make_class.
>>> def make_account_class():
"""Return the Account class, which has deposit and withdraw methods."""
def __init__(self, account_holder):
self['set']('holder', account_holder)
self['set']('balance', 0)
def deposit(self, amount):
"""Increase the account balance by amount and return the new balance."""
new_balance = self['get']('balance') + amount
self['set']('balance', new_balance)
return self['get']('balance')
def withdraw(self, amount):
"""Decrease the account balance by amount and return the new balance."""
balance = self['get']('balance')
if amount > balance:
return 'Insufficient funds'
self['set']('balance', balance - amount)
return self['get']('balance')
return make_class({'__init__': __init__,
'deposit': deposit,
'withdraw': withdraw,
'interest': 0.02})Dans cette fonction, les noms des attributs sont définis à la fin. Contrairement à une déclaration class de Python, qui impose la cohérence entre les noms de fonctions intrinsèques et les noms d'attributs, nous devons spécifier ici la correspondance entre les noms d'attributs et les valeurs manuellement.
La classe Account est finalement instanciée via l'affectation.
>>> Account = make_account_class()Ensuite, une instance de compte est créée via le message new, ce qui nécessite un nom pour aller avec le compte nouvellement créé.
>>> jim_acct = Account['new']('Jim')Ensuite, des messages get transmis à jim_acct permettent de récupérer les propriétés et les méthodes. Des méthodes peuvent être appelées pour mettre à jour le solde du compte.
>>> jim_acct['get']('holder')
'Jim'
>>> jim_acct['get']('interest')
0.02
>>> jim_acct['get']('deposit')(20)
20
>>> jim_acct['get']('withdraw')(5)
15Comme avec le système objet de Python, la définition d'un attribut d'une instance ne modifie pas l'attribut correspondant de sa classe.
>>> jim_acct['set']('interest', 0.04)
>>> Account['get']('interest')
0.02Héritage. Nous pouvons créer une classe fille CheckingAccount en surchargeant un sous-ensemble des attributs de la classe. Dans ce cas, nous modifions la méthode withdraw pour percevoir la commission et nous réduisons le taux d'intérêt.
>>> def make_checking_account_class():
"""Return the CheckingAccount class, which imposes a $1 withdrawal fee."""
def withdraw(self, amount):
return Account['get']('withdraw')(self, amount + 1)
return make_class({'withdraw': withdraw, 'interest': 0.01}, Account)Dans cette implémentation, nous appelons la fonction withdraw de la classe de base Account de la fonction de withdraw de la sous-classe, comme nous le ferions dans le système d'objets intégré de Python. Nous pouvons créer la sous-classe elle-même et une instance, comme précédemment :
>>> CheckingAccount = make_checking_account_class()
>>> jack_acct = CheckingAccount['new']('Jack')Les dépôts se comportent de manière identique, tout comme le constructeur. Les retraits donnent lieu aux frais de 1 $ grâce à la méthode withdraw spécialisée, et interest prend la nouvelle valeur inférieure de CheckingAccount.
>>> jack_acct['get']('interest')
0.01
>>> jack_acct['get']('deposit')(20)
20
>>> jack_acct['get']('withdraw')(5)
14Notre système d'objets basé sur des dictionnaires est assez similaire dans sa mise en œuvre au système d'objets intégré de Python. En Python, toute instance d'une classe définie par l'utilisateur a un attribut spécial __dict__ qui stocke les attributs locaux d'instance pour cet objet dans un dictionnaire, un peu comme notre dictionnaire attributes. Python diffère parce qu'il distingue certaines méthodes spéciales qui interagissent avec les fonctions intégrées pour s'assurer que ces fonctions se comportent correctement pour les arguments de nombreux types différents. Les fonctions qui fonctionnent sur différents types font l'objet de la section suivante.
7. Opérations génériques ▲
Dans ce chapitre, nous avons présenté les valeurs de données composées, ainsi que la technique d'abstraction des données à l'aide de constructeurs et de sélecteurs. En utilisant le passage de message, nous avons doté directement nos types de données abstraits d'un comportement. En utilisant la métaphore de l'objet, nous avons regroupé la représentation des données et les méthodes utilisées pour manipuler ces données afin de modulariser les programmes pilotés par les données avec l'état local.
Cependant, nous devons encore montrer que notre système d'objets nous permet de combiner différents types d'objets de manière flexible dans un grand programme. Le passage de message via des expressions pointées n'est qu'une façon de créer des expressions combinées avec plusieurs objets. Dans cette section, nous explorons d'autres méthodes pour combiner et manipuler des objets de différents types.
7-1. Conversion de chaîne ▲
Nous avons indiqué au début de ce tutoriel qu'une valeur d'objet devrait se comporter comme le type de données qu'elle est censée représenter, y compris produire une représentation de lui-même sous la forme d'une chaîne de caractères. Les représentations sous forme de chaîne de valeurs de données sont particulièrement importantes dans un langage interactif tel que Python, où la boucle read-eval-print nécessite que chaque valeur ait une sorte de représentation sous forme de chaîne.
Les valeurs de chaîne fournissent un moyen fondamental de communication de l'information entre les humains. Les séquences de caractères peuvent être affichées à l'écran, imprimées sur du papier, lues à haute voix, converties en braille ou transmises en morse. Les chaînes sont également fondamentales pour la programmation, car elles peuvent représenter des expressions Python. Pour un objet, nous souhaitons générer une chaîne qui, lorsqu'elle est interprétée comme une expression Python, est évaluée en un objet équivalent.
Python stipule que tous les objets doivent produire deux représentations distinctes des chaînes : une qui est un texte interprétable par un humain et une qui est une expression interprétable par Python. La fonction de construction des chaînes, str, renvoie une chaîne lisible par l'homme. Lorsque cela est possible, la fonction repr renvoie une expression Python qui évalue un objet égal. La docstring pour repr explique cette propriété :
repr(object) -> string
Return the canonical string representation of the object.
For most object types, eval(repr(object)) == object.Le résultat de l'appel de repr sur la valeur d'une expression est ce que Python imprime dans une session interactive.
>>> 12e12
12000000000000.0
>>> print(repr(12e12))
12000000000000.0Dans les cas où il n'existe aucune représentation qui évalue à la valeur d'origine, Python produit un proxy.
Le constructeur str coïncide souvent avec repr, mais fournit une représentation de texte plus interprétable dans certains cas. Par exemple, nous voyons une différence entre str et repr avec des dates :
>>> from datetime import date
>>> today = date(2011, 9, 12)
>>> repr(today)
'datetime.date(2011, 9, 12)'
>>> str(today)
'2011-09-12'Définir la fonction repr présente un nouveau défi : nous aimerions qu'elle s'applique correctement à tous les types de données, même ceux qui n'existaient pas lorsque repr a été implémentée. Nous aimerions que ce soit une fonction polymorphe, c'est-à-dire qui peut être appliquée à de nombreuses (poly) formes (morph) différentes de données.
Le passage de message fournit une solution élégante dans ce cas : la fonction repr invoque une méthode appelée __repr__ sur son argument.
>>> today.__repr__()
'datetime.date(2011, 9, 12)'En implémentant cette même méthode dans des classes définies par l'utilisateur, nous pouvons étendre l'applicabilité de repr à n'importe quelle classe que nous créons à l'avenir. Cet exemple met en évidence un autre avantage du passage de messages en général, à savoir qu'il fournit un mécanisme pour étendre le domaine des fonctions existantes à de nouveaux types d'objets.
Le constructeur str est implémenté d'une manière analogue : il appelle une méthode appelée __str__ sur son argument.
>>> today.__str__()
'2011-09-12'Ces fonctions polymorphes sont des exemples d'un principe plus général : certaines fonctions doivent s'appliquer à plusieurs types de données. L'approche de passage de message illustrée ici n'est qu'un exemple d'une famille de techniques pour mettre en œuvre des fonctions polymorphes. Le reste de cette section explore certaines alternatives.
7-2. Représentations multiples ▲
L'abstraction de données, qu'elle utilise des objets ou des fonctions, est un outil puissant pour gérer la complexité. Les types de données abstraits nous permettent de construire une barrière d'abstraction entre la représentation sous-jacente des données et les fonctions ou messages utilisés pour la manipuler. Cependant, dans les grands programmes, parler de « la représentation sous-jacente » d'un type de données dans un programme n'a pas toujours de sens. D'une part, il peut y avoir plus d'une représentation utile pour un objet de données, et nous aimerions peut-être concevoir des systèmes capables de gérer plusieurs représentations.
Pour prendre un exemple simple, les nombres complexes peuvent être représentés de deux manières presque équivalentes : sous la forme algébrique (parties réelle et imaginaire) et sous la forme polaire (module et angle). Parfois, la forme algébrique est plus appropriée et c'est parfois la forme polaire qui est la plus appropriée. En effet, il est parfaitement plausible d'imaginer un système dans lequel les nombres complexes sont représentés des deux manières, et dans lequel les fonctions de manipulation des nombres complexes fonctionnent avec l'une ou l'autre représentation.
Il y a un point plus important encore. Les grands systèmes logiciels sont souvent conçus par de nombreuses personnes travaillant sur de longues périodes, soumises à des exigences qui changent au fil du temps. Dans un tel environnement, il n'est tout simplement pas possible que tout le monde convienne à l'avance des choix de représentation des données. En plus des barrières d'abstraction des données qui isolent la représentation de l'utilisation, nous avons besoin de barrières d'abstraction qui isolent les différents choix de conception les uns des autres et permettent à différents choix de coexister dans un même programme. En outre, étant donné que les grands programmes sont souvent créés en combinant des modules préexistants conçus isolément, nous avons besoin de conventions qui permettent aux programmeurs d'intégrer des modules dans des systèmes plus importants, sans avoir besoin de revoir ou de réécrire ces modules.
Nous commençons par l'exemple simple des nombres complexes. Nous verrons comment le passage de messages nous permet de concevoir des représentations algébriques et polaires distinctes pour des nombres complexes tout en maintenant la notion d'un objet abstrait de type « nombre complexe ». Nous allons y parvenir en définissant des fonctions arithmétiques pour les nombres complexes (add_complex, mul_complex) en termes de sélecteurs génériques qui accèdent à des parties d'un nombre complexe indépendamment de la façon dont le nombre est représenté. Le système de nombres complexes qui en résulte contient deux types différents de barrières d'abstraction. Elles isolent les opérations de niveau supérieur des représentations de niveau inférieur. En outre, il existe une barrière verticale qui nous permet de concevoir séparément des représentations alternatives.

Notons au passage que nous développons un système qui effectue des opérations arithmétiques sur des nombres complexes comme un exemple simple, mais irréaliste d'un programme qui utilise des opérations génériques. Le type nombre complexe existe déjà en Python, mais pour cet exemple nous allons mettre en place le nôtre.
Comme les nombres rationnels, les nombres complexes sont naturellement représentés comme des paires. L'ensemble des nombres complexes peut être considéré comme un espace à deux dimensions avec deux axes orthogonaux, l'axe réel et l'axe imaginaire. De ce point de vue, le nombre complexe z = x + y * i (avec i*i = -1) peut être considéré comme le point dans le plan dont la coordonnée réelle est x et dont la coordonnée imaginaire est y. L'ajout de nombres complexes implique l'ajout de leurs coordonnées x et y respectives.
Lorsque l'on multiplie des nombres complexes, il est plus naturel de penser en termes de représentation d'un nombre complexe sous la forme polaire, en tant que module (magnitude) et angle. Le produit de deux nombres complexes est le vecteur obtenu en étirant un nombre complexe d'un facteur de la longueur de l'autre, puis en le faisant pivoter de l'angle de l'autre.
Ainsi, il existe deux représentations différentes pour les nombres complexes, qui sont appropriées pour différentes opérations. Cependant, du point de vue de quelqu'un qui écrit un programme utilisant des nombres complexes, le principe de l'abstraction des données suggère que toutes les opérations de manipulation de nombres complexes devraient être disponibles, quelle que soit la représentation utilisée par l'ordinateur.
Interfaces. Le passage de message fournit non seulement une méthode pour coupler le comportement et les données, mais il permet également à différents types de données de répondre au même message de différentes manières. Un message partagé qui suscite un comportement similaire de différentes classes d'objets est une méthode puissante d'abstraction.
Comme nous l'avons vu, un type de données abstrait est défini par des constructeurs, des sélecteurs et des conditions de comportement supplémentaires. Un concept étroitement lié est celui d'une interface, qui est un ensemble de messages partagés, avec une spécification de ce qu'ils signifient. Les objets qui répondent aux méthodes spéciales __repr__ et __str__ implémentent tous une interface commune de types pouvant être représentés en tant que chaînes.
Dans le cas de nombres complexes, l'interface nécessaire à l'implémentation de l'arithmétique consiste en quatre messages : real, imag, magnitude et angle. Nous pouvons implémenter l'addition et la multiplication en termes de ces messages.
Nous pouvons avoir deux types de données abstraits différents pour des nombres complexes qui diffèrent dans leurs constructeurs.
- ComplexRI construit un nombre complexe à partir de parties réelles et imaginaires.
- ComplexMA construit un nombre complexe à partir d'un module et d'un angle.
Avec ces messages et constructeurs, nous pouvons implémenter l'arithmétique complexe.
>>> def add_complex(z1, z2):
return ComplexRI(z1.real + z2.real, z1.imag + z2.imag)
>>> def mul_complex(z1, z2):
return ComplexMA(z1.magnitude * z2.magnitude, z1.angle + z2.angle)La relation entre les termes « type de données abstrait » (abstract data type - ADT) et « interface » est subtile. Un ADT comprend des moyens de construire des types de données complexes, en les manipulant comme des unités et en sélectionnant leurs composants. Dans un système orienté objet, un ADT correspond à une classe, bien que nous ayons vu qu'un système objet n'est pas nécessaire pour implémenter un ADT. Une interface est un ensemble de messages qui ont des significations associées et qui peuvent ou non inclure des sélecteurs. Conceptuellement, un ADT décrit une abstraction représentationnelle complète de quelque chose, alors qu'une interface spécifie un ensemble de comportements qui peuvent être partagés entre plusieurs choses.
Propriétés. Nous aimerions utiliser les deux types de nombres complexes de façon interchangeable, mais il serait peu efficace de stocker des informations redondantes sur chaque nombre. Nous aimerions stocker soit la représentation réelle-imaginaire, soit la représentation module-angle.
Python a une fonction simple pour calculer les attributs à la volée à partir de fonctions à zéro argument. Le décorateur @property permet aux fonctions d'être appelées sans la syntaxe d'appel standard. Une implémentation de nombres complexes en termes de parties réelles et imaginaires illustre ce point.
>>> from math import atan2
>>> class ComplexRI(object):
def __init__(self, real, imag):
self.real = real
self.imag = imag
@property
def magnitude(self):
return (self.real ** 2 + self.imag ** 2) ** 0.5
@property
def angle(self):
return atan2(self.imag, self.real)
def __repr__(self):
return 'ComplexRI({0}, {1})'.format(self.real, self.imag)Une seconde implémentation utilisant le module et l'angle fournit la même interface, car elle répond au même ensemble de messages.
>>> from math import sin, cos
>>> class ComplexMA(object):
def __init__(self, magnitude, angle):
self.magnitude = magnitude
self.angle = angle
@property
def real(self):
return self.magnitude * cos(self.angle)
@property
def imag(self):
return self.magnitude * sin(self.angle)
def __repr__(self):
return 'ComplexMA({0}, {1})'.format(self.magnitude, self.angle)En fait, nos implémentations de add_complex et mul_complex sont maintenant terminées ; l'une ou l'autre classe de nombres complexes peut être utilisée pour l'un ou l'autre argument dans l'une ou l'autre des fonctions arithmétiques complexes. Il convient de noter que le système objet ne relie pas explicitement les deux types complexes de quelque manière que ce soit (par exemple, par héritage). Nous avons implémenté l'abstraction des nombres complexes en partageant un ensemble commun de messages, une interface, entre les deux classes.
>>> from math import pi
>>> add_complex(ComplexRI(1, 2), ComplexMA(2, pi/2))
ComplexRI(1.0000000000000002, 4.0)
>>> mul_complex(ComplexRI(0, 1), ComplexRI(0, 1))
ComplexMA(1.0, 3.141592653589793)L'approche d'interface pour coder des représentations multiples a des propriétés attrayantes. La classe pour chaque représentation peut être développée séparément ; ces classes doivent seulement s'entendre sur les noms des attributs qu'ils partagent. L'interface est également additive. Si un autre programmeur voulait ajouter une troisième représentation de nombres complexes au même programme, il n'aurait qu'à créer une autre classe avec les mêmes attributs.
Méthodes spéciales. Les opérateurs mathématiques intégrés peuvent être étendus de la même manière que repr ; il existe des noms de méthodes spéciaux correspondant aux opérateurs Python pour les opérations arithmétiques, logiques et séquentielles.
Pour rendre notre code plus lisible, nous aimerions peut-être utiliser les opérateurs + et * directement lors de l'addition et de la multiplication de nombres complexes. L'ajout des méthodes suivantes à nos deux classes de nombres complexes permettra d'utiliser ces opérateurs, ainsi que les fonctions add et mul dans le module operator :
>>> ComplexRI.__add__ = lambda self, other: add_complex(self, other)
>>> ComplexMA.__add__ = lambda self, other: add_complex(self, other)
>>> ComplexRI.__mul__ = lambda self, other: mul_complex(self, other)
>>> ComplexMA.__mul__ = lambda self, other: mul_complex(self, other)Maintenant, nous pouvons utiliser la notation infixée avec nos classes définies par l'utilisateur :
>>> ComplexRI(1, 2) + ComplexMA(2, 0)
ComplexRI(3.0, 2.0)
>>> ComplexRI(0, 1) * ComplexRI(0, 1)
ComplexMA(1.0, 3.141592653589793)Lectures complémentaires. Pour évaluer les expressions contenant l'opérateur +, Python recherche des méthodes spéciales sur les opérandes gauche et droite de l'expression. Tout d'abord, Python vérifie une méthode __add__ sur la valeur de l'opérande de gauche, puis recherche une méthode __radd__ sur la valeur de l'opérande de droite. Si l'un ou l'autre est trouvé, cette méthode est invoquée avec la valeur de l'autre opérande comme argument.
Des protocoles similaires existent pour évaluer les expressions qui contiennent n'importe quel type d'opérateur en Python, y compris les notations de tranche et les opérateurs booléens. La documentation Python liste l'ensemble exhaustif de noms de méthodes pour les opérateurs. Le livre Dive into Python 3 a un chapitre sur les noms de méthodes spéciales qui décrit de nombreux détails de leur utilisation dans l'interpréteur Python.
7-3. Fonctions génériques ▲
Notre implémentation de nombres complexes a rendu deux types de données interchangeables en tant qu'arguments des fonctions add_complex et mul_complex. Nous allons maintenant voir comment utiliser cette même idée non seulement pour définir des opérations qui sont génériques sur différentes représentations, mais aussi pour définir des opérations qui sont génériques sur différents types d'arguments qui ne partagent pas une interface commune.
Les opérations que nous avons définies jusqu'à présent traitent les différents types de données comme étant complètement indépendants. Ainsi, il existe des paquets distincts pour ajouter, disons, deux nombres rationnels, ou deux nombres complexes. Ce que nous n'avons pas encore considéré est le fait qu'il est sensé de définir des opérations qui traversent les frontières de type, telles que l'addition d'un nombre complexe à un nombre rationnel. Nous nous sommes donné beaucoup de mal pour introduire des barrières entre les parties de nos programmes afin qu'ils puissent être développés et compris séparément.
Nous aimerions introduire les opérations de type croisé d'une manière soigneusement contrôlée, afin que nous puissions les supporter sans violer sérieusement nos barrières d'abstraction. Il y a une forme de contradiction entre les résultats que nous désirons : nous aimerions pouvoir ajouter un nombre complexe à un nombre rationnel, et nous aimerions le faire en utilisant une fonction add générique capable de faire ce qu'il faut avec tous les types numériques. Dans le même temps, nous aimerions séparer les problèmes de nombres complexes et des problèmes de nombres rationnels chaque fois que c'est possible, afin de maintenir un programme modulaire.
Reprenons notre implémentation des nombres rationnels pour utiliser le système d'objet intégré de Python. Comme précédemment, nous allons stocker un nombre rationnel comme un numérateur et un dénominateur sous forme de fraction simplifiée.
>>> from fractions import gcd
>>> class Rational(object):
def __init__(self, numer, denom):
g = gcd(numer, denom)
self.numer = numer // g
self.denom = denom // g
def __repr__(self):
return 'Rational({0}, {1})'.format(self.numer, self.denom)Ajouter et multiplier les nombres rationnels dans cette nouvelle implémentation se fait comme précédemment.
>>> def add_rational(x, y):
nx, dx = x.numer, x.denom
ny, dy = y.numer, y.denom
return Rational(nx * dy + ny * dx, dx * dy)
>>> def mul_rational(x, y):
return Rational(x.numer * y.numer, x.denom * y.denom)Résolution de type. Une façon de gérer les opérations avec des types croisés est de concevoir une fonction différente pour chaque combinaison possible de types pour lesquels l'opération est valide. Par exemple, nous pourrions étendre notre implémentation de nombres complexes afin qu'elle fournisse une fonction permettant d'ajouter des nombres complexes à des nombres rationnels. Nous pouvons fournir cette fonctionnalité de manière générique en utilisant une technique appelée résolution de type (dispatching on type).
L'idée consiste à écrire des fonctions qui inspectent d'abord le type d'argument reçu, puis exécuter le code approprié pour le type. En Python, le type d'un objet peut être inspecté avec la fonction type intégrée.
>>> def iscomplex(z):
return type(z) in (ComplexRI, ComplexMA)
>>> def isrational(z):
return type(z) == RationalDans ce cas, nous nous appuyons sur le fait que chaque objet connaît son type, et nous pouvons rechercher ce type en utilisant la fonction de type Python. Même si la fonction type n'était pas disponible, nous pourrions imaginer implémenter iscomplex et isrational en termes d'un attribut de classe partagé pour Rational, ComplexRI et ComplexMA.
Considérons maintenant l'implémentation suivante de la fonction add, qui vérifie explicitement le type des deux arguments. Nous n'utiliserons pas les méthodes spéciales de Python (à savoir __add__) dans cet exemple.
>>> def add_complex_and_rational(z, r):
return ComplexRI(z.real + r.numer/r.denom, z.imag)
>>> def add(z1, z2):
"""Add z1 and z2, which may be complex or rational."""
if iscomplex(z1) and iscomplex(z2):
return add_complex(z1, z2)
elif iscomplex(z1) and isrational(z2):
return add_complex_and_rational(z1, z2)
elif isrational(z1) and iscomplex(z2):
return add_complex_and_rational(z2, z1)
else:
return add_rational(z1, z2)Cette approche simpliste de la résolution de type, qui utilise une grande instruction conditionnelle, n'est pas additive. Si un autre type numérique était inclus dans le programme, nous devions ré-implémenter add avec de nouvelles clauses.
Nous pouvons créer une implémentation plus flexible de la fonction add en implémentant la résolution de type via un dictionnaire. La première étape de l'extension de la flexibilité d'add sera de créer dans nos classes un ensemble d'étiquettes qui masque les deux implémentations distinctes des nombres complexes.
>>> def type_tag(x):
return type_tag.tags[type(x)]
>>> type_tag.tags = {ComplexRI: 'com', ComplexMA: 'com', Rational: 'rat'}Ensuite, nous utilisons ces étiquettes de type pour indexer un dictionnaire qui stocke les différentes façons d'ajouter des nombres. Les clés du dictionnaire sont des tuples d'étiquettes de type, et les valeurs sont des fonctions d'addition spécifiques au type.
>>> def add(z1, z2):
types = (type_tag(z1), type_tag(z2))
return add.implementations[types](z1, z2)Cette définition d' add n'a aucune fonctionnalité en elle-même ; elle repose entièrement sur un dictionnaire appelé add.implementations pour implémenter l'addition. Nous pouvons alimenter ce dictionnaire comme suit.
>>> add.implementations = {}
>>> add.implementations[('com', 'com')] = add_complex
>>> add.implementations[('com', 'rat')] = add_complex_and_rational
>>> add.implementations[('rat', 'com')] = lambda x, y: add_complex_and_rational(y, x)
>>> add.implementations[('rat', 'rat')] = add_rationalCette approche de la résolution de type basée sur un dictionnaire est additive, car add.implementations et type_tag.tags peuvent toujours être étendus. Tout nouveau type numérique peut « s'installer » dans le système existant en ajoutant de nouvelles entrées à ces dictionnaires.
Bien que nous ayons introduit une certaine complexité dans le système, nous avons maintenant une fonction add générique et extensible qui gère les types mixtes.
>>> add(ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> add(Rational(5, 3), Rational(1, 2))
Rational(13, 6)Programmation orientée données. Notre mise en œuvre d'add fondée sur un dictionnaire n'est pas du tout spécifique à l'addition ; elle ne contient directement aucune logique d'addition. Elle implémente l'addition seulement parce que nous avons alimenté son dictionnaire d'implementations avec des fonctions qui effectuent l'addition.
Une version plus générale de l'arithmétique générique appliquerait des opérateurs arbitraires à des types arbitraires et utiliserait un dictionnaire pour stocker les implémentations de diverses combinaisons. Cette approche entièrement générique de la mise en œuvre des méthodes est appelée programmation orientée données. Dans notre cas, nous pouvons implémenter à la fois l'addition générique et la multiplication sans logique redondante.
>>> def apply(operator_name, x, y):
tags = (type_tag(x), type_tag(y))
key = (operator_name, tags)
return apply.implementations[key](x, y)Dans cette fonction générique apply, une clé est construite à partir du nom de l'opérateur (par exemple, 'add') et un tuple d'étiquettes de type pour les arguments. Les implémentations sont également alimentées à l'aide de ces étiquettes. Cela nous permet de mettre en place la multiplication sur les nombres complexes et rationnels :
>>> def mul_complex_and_rational(z, r):
return ComplexMA(z.magnitude * r.numer / r.denom, z.angle)
>>> mul_rational_and_complex = lambda r, z: mul_complex_and_rational(z, r)
>>> apply.implementations = {('mul', ('com', 'com')): mul_complex,
('mul', ('com', 'rat')): mul_complex_and_rational,
('mul', ('rat', 'com')): mul_rational_and_complex,
('mul', ('rat', 'rat')): mul_rational}Nous pouvons également ajouter à apply les implémentations complémentaires d'add, en utilisant la méthode update des dictionnaires :
>>> adders = add.implementations.items()
>>> apply.implementations.update({('add', tags):fn for (tags, fn) in adders})Maintenant que la fonction apply prend en charge huit implémentations différentes dans une seule table, nous pouvons l'utiliser pour manipuler des nombres rationnels et complexes de manière assez générique.
>>> apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1)Cette approche orientée données gère la complexité des opérateurs de type croisé, mais elle est lourde. Avec un tel système, le coût de l'introduction d'un nouveau type n'est pas seulement celui de l'écriture des méthodes pour ce type, mais aussi la construction et l'installation des fonctions qui mettent en œuvre les opérations de type croisé. Cette charge peut facilement exiger beaucoup plus de code que ce qui est nécessaire pour définir les opérations sur le type lui-même.
Les techniques de résolution de type et de programmation orientée données créent des implémentations additives de fonctions génériques, mais elles ne séparent pas efficacement les problèmes de mise en œuvre ; les développeurs des types numériques individuels doivent prendre en compte d'autres types lors de l'écriture d'opérations de type croisé. La combinaison de nombres rationnels et de nombres complexes n'est pas strictement le domaine de l'un ou l'autre type. La formulation de politiques cohérentes sur la répartition des responsabilités entre les types peut être une tâche écrasante dans la conception de systèmes ayant de nombreux types et opérations de type croisé.
Coercition. Dans la situation générale d'opérations complètement indépendantes agissant sur des types complètement indépendants, la mise en œuvre d'opérations croisées explicites, aussi lourde soit-elle, est le mieux que l'on puisse espérer. Heureusement, nous pouvons parfois faire mieux en profitant de la structure supplémentaire qui peut être latente dans notre système de types. Souvent, les différents types de données ne sont pas complètement indépendants, et il peut y avoir des moyens par lesquels les objets d'un type peuvent être considérés comme étant d'un autre type. Ce processus s'appelle la coercition. Par exemple, si on nous demande de combiner arithmétiquement un nombre rationnel avec un nombre complexe, nous pouvons considérer le nombre rationnel comme un nombre complexe dont la partie imaginaire est nulle. Ce faisant, nous transformons le problème en celui de combiner deux nombres complexes, qui peut être traité de la manière ordinaire par add_complex et mul_complex.
En général, nous pouvons implémenter cette idée en concevant des fonctions de coercition qui transforment un objet d'un type en un objet équivalent d'un autre type. Voici une fonction de coercition qui transforme un nombre rationnel en un nombre complexe avec une partie imaginaire nulle :
>>> def rational_to_complex(x):
return ComplexRI(x.numer/x.denom, 0)Maintenant, nous pouvons définir un dictionnaire des fonctions de coercition. Ce dictionnaire pourrait être étendu à mesure que d'autres types numériques sont introduits.
>>> coercions = {('rat', 'com'): rational_to_complex}Il n'est généralement pas possible de convertir un objet quelconque de chaque type dans chacun des autres types. Par exemple, il n'y a aucun moyen de convertir un nombre complexe quelconque en un nombre rationnel ; donc ce type de conversion ne figurera pas dans le dictionnaire coercions.
En utilisant le dictionnaire coercions, nous pouvons écrire une fonction appelée coerce_apply qui tente de convertir des arguments dans des valeurs du même type, et applique ensuite un opérateur. Le dictionnaire d'implémentations de coerce_apply n'inclut aucune implémentation d'opérateur de type croisé.
>>> def coerce_apply(operator_name, x, y):
tx, ty = type_tag(x), type_tag(y)
if tx != ty:
if (tx, ty) in coercions:
tx, x = ty, coercions[(tx, ty)](x)
elif (ty, tx) in coercions:
ty, y = tx, coercions[(ty, tx)](y)
else:
return 'No coercion possible.'
key = (operator_name, tx)
return coerce_apply.implementations[key](x, y)Les implementations de coerce_apply ne nécessitent qu'une seule étiquette de type, car elles supposent que les deux valeurs partagent la même étiquette de type. Par conséquent, nous n'avons besoin que de quatre implémentations pour prendre en charge l'arithmétique générique sur les nombres complexes et rationnels.
>>> coerce_apply.implementations = {('mul', 'com'): mul_complex,
('mul', 'rat'): mul_rational,
('add', 'com'): add_complex,
('add', 'rat'): add_rational}Avec ces implémentations en place, coerce_apply peut remplacer apply.
>>> coerce_apply('add', ComplexRI(1.5, 0), Rational(3, 2))
ComplexRI(3.0, 0)
>>> coerce_apply('mul', Rational(1, 2), ComplexMA(10, 1))
ComplexMA(5.0, 1.0)Ce schéma de coercition présente certains avantages par rapport à la définition explicite des opérations de type croisé. Bien que nous ayons encore besoin d'écrire des fonctions de coercition pour relier les types, nous devons écrire une seule fonction pour chaque paire de types plutôt qu'une fonction différente pour chaque collection de types et chaque opération générique. Nous comptons ici sur le fait que la transformation appropriée entre les types dépend uniquement des types eux-mêmes, et non de l'opération particulière à appliquer.
D'autres avantages viennent de l'extension de la coercition. Certains schémas de coercition plus sophistiqués n'essaient pas seulement de convertir un type en un autre, mais plutôt d'essayer de convertir deux types différents en un troisième type commun. Considérons un losange et un rectangle : aucun des deux n'est un cas particulier de l'autre, mais les deux peuvent être considérés comme des quadrilatères. Une autre extension de la coercition est la coercition itérative, dans laquelle un type de données est forcé dans un autre via des types intermédiaires. Considérons qu'un entier peut être converti en un nombre réel en le convertissant d'abord en un nombre rationnel, puis en convertissant ce nombre rationnel en un nombre réel. L'enchaînement de contraintes de cette manière peut réduire le nombre total de fonctions de coercition requises par un programme.
Malgré ses avantages, la coercition présente des inconvénients potentiels. D'une part, les fonctions de coercition peuvent faire perdre des informations lorsqu'elles sont appliquées. Dans notre exemple, les nombres rationnels sont des représentations exactes, mais deviennent des approximations lorsqu'ils sont convertis en nombres complexes.
Certains langages de programmation ont des systèmes de coercition automatique intégrés. D'ailleurs, les premières versions de Python avaient une méthode spéciale __coerce__ sur les objets. En fin de compte, la complexité du système de coercition intégré ne justifiait pas son utilisation, et cette méthode spéciale a donc été supprimée. Au lieu de cela, les opérateurs particuliers appliquent la coercition à leurs arguments si nécessaire. Les opérateurs sont implémentés comme des appels de méthode sur les types définis par l'utilisateur en utilisant des méthodes spéciales comme __add__ et __mul__. C'est à vous, l'utilisateur, de décider si vous souhaitez utiliser la résolution de type, la programmation orientée données, le passage de message ou la coercition pour implémenter des fonctions génériques dans vos programmes.





