I. Processus d'optimisation▲
1. Faites-le fonctionner : écrivez le code de manière simple et lisible.
2. Faites-le fonctionner efficacement : écrivez des méthodes de contrôles automatisés, assurez-vous que votre algorithme est juste et que si vous le plantez, vos méthodes détecteront les erreurs.
3. Optimisez votre code en écrivant des méthodes capables de détecter et d'accélérer le traitement des goulots d'étranglement en trouvant un meilleur algorithme ou une meilleure mise en œuvre. Rappelez-vous que vous devez trouver un compromis entre l'étude d'un exemple réaliste d'une part et la simplicité et la performance de votre code d'autre part.
4. Pour un travail efficace, il vaut mieux travailler avec des processus d'inspection durant environ 10 secondes.
II. Étude d'un code Python▲
Pas d'optimisation possible sans contrôle de mesures !
- Mesurer : inspecter, chronométrer.
- Vous aurez des surprises : le code le plus rapide n'est pas toujours celui auquel vous pensez.
II-A. Timeit▲
Avec IPython, utilisez timeit (http://docs.python.org/library/timeit.html) pour chronométrer les instructions élémentaires :
In [1]: import numpy as np
In [2]: a = np.arange(1000)
In [3]: %timeit a ** 2
100000 loops, best of 3: 5.73 us per loop
In [4]: %timeit a ** 2.1
1000 loops, best of 3: 154 us per loop
In [5]: %timeit a * a
100000 loops, best of 3: 5.56 us per loopUtilisez-le pour guider vos choix entre plusieurs solutions.
Pour les appels de longue durée, utilisez %time au lieu de %timeit ; il est moins précis, mais plus rapide.
II-B. Profiler▲
Utile lorsque vous avez un long programme à étudier, par exemple le fichier suivant.
# For this example to run, you also need the 'ica.py' file
import numpy as np
from scipy import linalg
from ica import fastica
def test():
data = np.random.random((5000, 100))
u, s, v = linalg.svd(data)
pca = np.dot(u[:, :10].T, data)
results = fastica(pca.T, whiten=False)
if __name__ == '__main__':
test()Il s'agit de la combinaison de deux techniques fondamentales d'enseignement :
PCA est une méthode de réduction des dimensions, par exemple un algorithme conçu pour expliquer les fluctuations de données en utilisant moins de dimensions.
ICA est une méthode de séparation des sources, par exemple pour isoler plusieurs signaux enregistrés par plusieurs capteurs. Pour plus d'informations, consultez : l'exemple FastICA de scikits-learn.
Pour l'exécuter, vous aurez aussi besoin de télécharger le module ICA. Dans Ipython, nous pouvons chronométrer le script :
In [1]: %run -t demo.py
IPython CPU timings (estimated):
User : 14.3929 s.
System: 0.256016 s.et l'inspecter :
In [2]: %run -p demo.py
916 function calls in 14.551 CPU seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
1 14.457 14.457 14.479 14.479 decomp.py:849(svd)
1 0.054 0.054 0.054 0.054 {method 'random_sample' of 'mtrand.RandomState' objects}
1 0.017 0.017 0.021 0.021 function_base.py:645(asarray_chkfinite)
54 0.011 0.000 0.011 0.000 {numpy.core._dotblas.dot}
2 0.005 0.002 0.005 0.002 {method 'any' of 'numpy.ndarray' objects}
6 0.001 0.000 0.001 0.000 ica.py:195(gprime)
6 0.001 0.000 0.001 0.000 ica.py:192(g)
14 0.001 0.000 0.001 0.000 {numpy.linalg.lapack_lite.dsyevd}
19 0.001 0.000 0.001 0.000 twodim_base.py:204(diag)
1 0.001 0.001 0.008 0.008 ica.py:69(_ica_par)
1 0.001 0.001 14.551 14.551 {execfile}
107 0.000 0.000 0.001 0.000 defmatrix.py:239(__array_finalize__)
7 0.000 0.000 0.004 0.001 ica.py:58(_sym_decorrelation)
7 0.000 0.000 0.002 0.000 linalg.py:841(eigh)
172 0.000 0.000 0.000 0.000 {isinstance}
1 0.000 0.000 14.551 14.551 demo.py:1(<module>)
29 0.000 0.000 0.000 0.000 numeric.py:180(asarray)
35 0.000 0.000 0.000 0.000 defmatrix.py:193(__new__)
35 0.000 0.000 0.001 0.000 defmatrix.py:43(asmatrix)
21 0.000 0.000 0.001 0.000 defmatrix.py:287(__mul__)
41 0.000 0.000 0.000 0.000 {numpy.core.multiarray.zeros}
28 0.000 0.000 0.000 0.000 {method 'transpose' of 'numpy.ndarray' objects}
1 0.000 0.000 0.008 0.008 ica.py:97(fastica)
…De toute évidence, la SVD (dans decomp.py) est ce qui nous prend le plus de temps : c'est notre goulot d'étranglement. Nous devons trouver un moyen d'accélérer ou d'éviter (optimisation de l'algorithme) cette étape. Passer du temps sur le reste du code est inutile.
II-C. Line-profiler▲
L'outil d'inspection est formidable : il nous dit quelle fonction prend le plus de temps, mais pas où elle est appelée.
Pour cela, nous utilisons line_profiler : dans le fichier source, nous agrémentons les fonctions que nous voulons contrôler avec @profile (il n'est pas nécessaire de l'importer).
@profile
def test():
data = np.random.random((5000, 100))
u, s, v = linalg.svd(data)
pca = np.dot(u[: , :10], data)
results = fastica(pca.T, whiten=False)Puis nous exécutons le script en utilisant le programme kernprof.py, qui alterne entre -l, --line-by-line et -v, --view pour utiliser l'inspecteur ligne par ligne, voir les résultats et finalement les sauvegarder :
$ kernprof.py -l -v demo.py
Wrote profile results to demo.py.lprof
Timer unit: 1e-06 s
File: demo.py
Function: test at line 5
Total time: 14.2793 s
Line # Hits Time Per Hit % Time Line Contents
==============================================================
5 @profile
6 def test():
7 1 19015 19015.0 0.1 data = np.random.random((5000, 100))
8 1 14242163 14242163.0 99.7 u, s, v = linalg.svd(data)
9 1 10282 10282.0 0.1 pca = np.dot(u[:10, :], data)
10 1 7799 7799.0 0.1 results = fastica(pca.T, whiten=False)La SVD prend tout le temps ! Nous devons optimiser ce processus.
II-D. Exécuter cProfile▲
Dans l'exemple IPython précédent, IPython appelle simplement les inspecteurs Python cProfile et profile fournis à l'installation. Il pourrait vous être utile de visualiser les informations de l'inspecteur avec un autre outil.
$ python -m cProfile -o demo.prof demo.pyLe -o enverra les résultats obtenus par l'inspecteur dans le fichier demo.prof.
II-E. Utiliser gprof2dot▲
Si vous souhaitez obtenir une représentation plus visuelle des informations de l'inspecteur, vous pouvez utiliser l'outil gprof2dot :
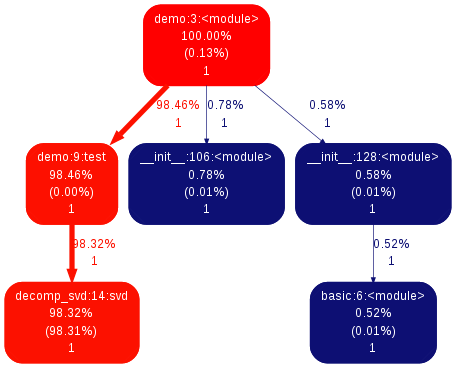
$ gprof2dot -f pstats demo.prof | dot -Tpng -o demo-prof.pngCela générera l'image suivante :
qui décrit ici une image semblable à notre précédent résultat.
III. Accélérer l'exécution du code▲
Maintenant que nous avons identifié les goulots d'étranglement, nous devons accélérer leurs codes.
III-A. Optimisation de l'algorithme▲
Le premier objectif à atteindre est l'optimisation de votre algorithme : existe-t-il des moyens de calculer moins, ou plus rapidement ?
Une bonne compréhension des mathématiques liées aux algorithmes permet d'avoir une bonne vue d'ensemble du problème. Cependant, il n'est pas rare de trouver des modifications simples, comme sortir d'une boucle FOR des calculs ou une allocation mémoire, ce qui permet d'obtenir des gains significatifs.
III-A-1. L'exemple de SVD▲
Dans les deux exemples précédents, la SVD décomposition en valeurs singulières est ce qui nous prend le plus de temps.
En effet, le coût de traitement de cet algorithme est environ n3 de la taille de la matrice fournie en entrée.
Toutefois, dans ces deux exemples, nous n'utilisons pas toutes les informations fournies par la SVD, mais seulement les premières lignes du premier argument renvoyé. Si nous utilisons la méthode SVD de scypy, nous pouvons demander une version incomplète de la SVD. Notez que les méthodes d'algèbre linéaire en scipy sont plus complètes que celles en numpy et devraient leur être préférées.
In [3]: %timeit np.linalg.svd(data)
1 loops, best of 3: 14.5 s per loop
In [4]: from scipy import linalg
In [5]: %timeit linalg.svd(data)
1 loops, best of 3: 14.2 s per loop
In [6]: %timeit linalg.svd(data, full_matrices=False)
1 loops, best of 3: 295 ms per loop
In [7]: %timeit np.linalg.svd(data, full_matrices=False)
1 loops, best of 3: 293 ms per loopNous pouvons donc utiliser ces résultats pour optimiser le code précédent :
In [1]: import demo
In [2]: %timeit demo.
demo.fastica demo.np demo.prof.pdf demo.py demo.pyc
demo.linalg demo.prof demo.prof.png demo.py.lprof demo.test
In [2]: %timeit demo.test()
ica.py:65: RuntimeWarning: invalid value encountered in sqrt
W = (u * np.diag(1.0/np.sqrt(s)) * u.T) * W # W = (W * W.T) ^{-1/2} * W
1 loops, best of 3: 17.5 s per loop
In [3]: import demo_opt
In [4]: %timeit demo_opt.test()
1 loops, best of 3: 208 ms per loopDes décompositions de valeurs singulières incomplètes sur des réels (ex. : calculer seulement les 10 premiers vecteurs propres) peuvent être réalisées avec arpack, disponible dans scipy.sparse.li, alg.eigsh.
Algèbre linéaire informatique
Pour certains algorithmes, beaucoup de goulots d'étranglement seront des calculs d'algèbre linéaire. Dans ce cas, la solution est d'utiliser la bonne fonction au bon moment. Par exemple, un problème de valeur propre est plus facile à résoudre avec une matrice symétrique plutôt qu'avec une matrice générale. De plus, bien souvent, vous pouvez éviter d'inverser une matrice et utiliser une opération moins gourmande.
Maîtrisez l'algèbre linéaire informatique. En cas de doute, explorez scipy.linalg et utilisez %timeit pour tester d'autres approches avec vos données.
III-A-2. Écrire du code numérique plus rapide▲
Vous pouvez trouver une analyse complète de l'utilisation avancée de numpy au chapitre Advanced Numpy, ou dans l'article The NumPy array : a structure for efficient numerical computation de van derWalt et al. Ici nous aborderons seulement quelques astuces fréquemment utilisées pour accélérer votre code.
- Méthodes de vectorisation pour les boucles
Trouvez des astuces pour éviter l'utilisation des tableaux numpy dans vos boucles. Pour ce faire, les masques et les tableaux d'indices pourront vous être utiles,
- Méthode de broadcast
Utilisez la méthode de broadcast pour réduire autant que possible les opérations sur les tableaux avant de les combiner.
- Les instructions « en place »
In [1]: a = np.zeros(1e7)
In [2]: %timeit global a ; a = 0*a
10 loops, best of 3: 111 ms per loop
In [3]: %timeit global a ; a *= 0
10 loops, best of 3: 48.4 ms per loopNous avons besoin de global a dans timeit pour qu'il puisse fonctionner en affectant la valeur a et l'utiliser comme une variable locale.
- Soyez économe en mémoire, utilisez des vues pas des copies
Copier de grands tableaux est aussi gourmand que de leur appliquer des opérations numériques simples :
In [1]: a = np.zeros(1e7)
In [2]: %timeit a.copy()
10 loops, best of 3: 124 ms per loop
In [3]: %timeit a + 1
10 loops, best of 3: 112 ms per loop- Attention aux effets de cache
Les accès mémoire sont plus légers lorsqu'ils sont groupés : accéder à un tableau de manière continue est plus rapide que de manière inopinée. Cela implique surtout que de plus petits traitements sont plus rapides (voir Les effets de cache CPU) :
In [1]: c = np.zeros((1e4, 1e4), order='C')
In [2]: %timeit c.sum(axis=0)
1 loops, best of 3: 3.89 s per loop
In [3]: %timeit c.sum(axis=1)
1 loops, best of 3: 188 ms per loop
In [4]: c.strides
Out[4]: (80000, 8)Voilà pourquoi les commandes Fortran ou C pourront faire une grande différence sur vos traitements :
In [5]: a = np.random.rand(20, 2**18)
In [6]: b = np.random.rand(20, 2**18)
In [7]: %timeit np.dot(b, a.T)
1 loops, best of 3: 194 ms per loop
In [8]: c = np.ascontiguousarray(a.T)
In [9]: %timeit np.dot(b, c)
10 loops, best of 3: 84.2 ms per loopNotez qu'il ne sera probablement pas efficace de copier les données pour contourner ce problème.
In [10]: %timeit c = np.ascontiguousarray(a.T)
10 loops, best of 3: 106 ms per loopL'utilisation de numexpr peut être utile pour optimiser automatiquement votre code afin de parer à ce genre d'effets
- Utiliser du code compilé
Le dernier recours, une fois que vous êtes sûr d'avoir exploré toutes les autres méthodes d'optimisations, est de transformer les points problématiques (les quelques lignes ou fonctions qui prennent le plus de temps) en code compilé. Pour ce dernier, la meilleure option est d'utiliser Cython : il est facile de transformer du code Python sortant en code compilé, et une bonne utilisation de l'assistance numpy génère un code performant pour les tableaux numpy, en déroulant les boucles par exemple.
Pour toutes les solutions précédentes : inspectez et chronométrez vos choix. Ne basez pas votre optimisation sur des considérations théoriques.
IV. Liens supplémentaires▲
- Si vous avez besoin d'examiner l'utilisation de la mémoire, vous pouvez essayer l'inspecteur de mémoire.
- Si vous avez besoin d'inspecter des extensions C, vous pouvez utiliser gperftools de Python avec yep.
- Si vous voulez suivre les performances de votre code sur la durée (par exemple vous faites de nouveaux « commits » sur votre espace de stockage), vous pouvez utiliser vbench.
- Si vous avez besoin d'une représentation interactive, pourquoi ne pas utiliser RunSnakeRun ?
V. Remerciements▲
Merci aux personnes suivantes pour leur aide pour cette traduction :